توطئة:
تحدثنا في مقال سابق بعنوان “التطبيقات التربوية للنظرية البنائية الجزء الأول” عن إستراتيجية دورة التعلم: الثلاثية والرباعية والخماسية والسباعية ومن ثم تطرقنا لنموذج التعلم البنائي كأهم التطبيقات التربوية للنظرية البنائية. ويمكن للقارئ الاطلاع عليه من موقع تعليم جديد على هذا الرابط.
وفي هذا المقال الذي عنونته ب “التطبيقات التربوية للنظرية البنائية الجزء الثاني” سنتحدث باختصار عن: التعلم المبني على حل المشكلات، ونموذج ويتلي Wheatley للتعلم المتمركز حول المشكلة، ونموذج شكل V كتطبيقات تربوية مهمة للنظرية البنائية أيضا، وسنكمل السلسلة البحثية –إن شاء الله- عن باقي أهم الإستراتيجيات والنماذج التعليمية الأخرى والتي تعد أيضا من التطبيقات التربوية للنظرية البنائية. إننا في هذا المقال وسابقه وتاليه لن نأتي بجديد، فالنظرية البنائية وتطبيقاتها التربوية قد تناولها الفلاسفة والمنظرين والمختصين والباحثين في مجال العلوم التربوية على الصعيدين العالمي والعربي من خلال كتب تربوية أو دراسات علمية، وإنما تكمن إضافتنا العلمية هنا بوضعها بقالب موحد يجمع ويلخص ما كُتب حول النظرية وتطبيقاتها التربوية مع التوضيح بدروس تطبيقية نسقط عليها عمليا خطوات الإستراتيجيات والنماذج التعليمية المتوافقة مع أفكار النظرية البنائية.
التعلم المبني على حل المشكلات
تعود جذور التعلم المبني على حل المشكلات إلى الحركة التقدمية مستمدا جذوره الفكرية من فكر جون ديوي، والذي نادى بأهمية التعلم من خلال مخاطبة غريزة البحث والتكوين الطبيعي لدى الطلاب ومخاطبة المعلمين على التعليم وفق هذا الأساس. وقد كتب بأن التوجه أو المنحنى الأول لمعالجة أي موضوع في المدرسة إذا ما أريد إثارة التفكير فيه يجب أن يكون غير مدرسي قدر الإمكان، وبالنسبة لجون ديوي فإن خبرات الطلاب خارج المدرسة تزودنا بتلميحات مساعدة حول كيفية تعديل الدروس بناء على ما يثير اهتمام الطلاب ويشدهم لعملية التعلم (إبراهيم، 2009، 63). ويُعرف التعلم المبني على المشكلات بأنه إستراتيجية تعليمية تركز على الطالب كمحور للتعلم النشط، ويتميز باستخدام مشكلات العالم الحقيقية، ويتطلب المعرفة الناقدة، والبراعة في حل المشكلات، ومهارات الفريق المشارك، حيث أن المشكلة تقود عملية التعلم، مما يساعد في اكتشاف وتعلم المفاهيم والمبادئ الأساسية. ويكمن دور المعلم في التعلم المبني على حل المشكلات في مساندة الطلاب في أسئلتهم (إبراهيم، 2009، 65). وقد أسهم جان بياجيه وليف فايجوتسكي في تنمية مفهوم البنائية والذي يعتمد عليه قدر كبير من التعليم المعاصر المبني على المشكلات. حيث وأن المنظور المعرفي البنائي الذي يقوم عليه التعلم المبني على المشكلات يذهب الى أن المتعلمين في أي سن يندمجون اندماجا نشطا في عملية اكتساب المعلومات وفي بناء معرفتهم حيث تتطور هذه المعرفة على نحو مستمر وتتغير مع مواجهة المتعلمين بخبرات جديدة تجبرهم على بناء المعرفة السابقة وتعديلها (عبد الحميد، 1999). ويشير (Dellsile, 1997) المشار إليه في (إبراهيم، 2009، 69) إلى أن التعلم المبني على حل المشكلات يقدم للمعلمين في مختلف المراحل التعليمية طريقة منظمة لمساعدة طلابهم على بناء مهارات التفكير، كما أنها تتيح للطلاب مزيدا من الحرية وينقل الدور النشط في غرفة الصف إلى الطلاب من خلال المشاكل التي ترتبط بحياتهم وينغمسون معها عمليا ومن ثم يعيدون صياغتها.
خطوات التعلم المبني على حل المشكلات
يتألف التعلم المبني على حل المشكلات من خمس مراحل تعليمية أساسية تبدأ بتوجيه المعلم للطلاب نحو الموقف المشكل، وتنتهي بعرض عمل الطلاب وإنتاجهم وتحليله. يمكن تلخيصها بالاستفادة من (عبد الحميد، 1999، 141؛ إبراهيم، 2009، 72). كما يلي:
- الأولى: توجيه الطلاب نحو المشكلة، وفيها يراجع المعلم أهداف الدرس ويصف الآليات المتطلبة، ويثير دافعية الطلاب للاندماج في نشاط حل المشكلة المختارة.
- الثانية: تنظيم الطلاب للدرس، وفيها يساعد المعلم الطلاب على تعريف وتحديد مهام الدرس التي تتصل بالمشكلة.
- الثالثة: البحث المستقل والجماعي، وفيها يشجع المعلم الطلاب على جمع المعلومات المناسبة لحل المشكلة، وإجراء التجارب أو الخطط والسعي لبلوغ التفسيرات والتوصل إلى الحلول.
- الرابعة التوصل الى النتائج وعرضها، وفيها يساعد المعلم الطلاب في تخطيط النواتج وإعدادها.
- الخامسة: تحليل عملية حل المشكلة وتقويمها، وفيها يساعد المعلم الطلاب على تأمل بحوثهم واستقصاءاتهم والعمليات التي استخدموها.
ويذكر ستيفن وآخرين (Stepien et al, 1993) المشار إليه في (إبراهيم، 2009، 72) ثلاث مراحل للتعلم المبني على حل المشكلات وهي:
- الأولى: مواجهة وتحديد المشكلة، وفيها يواجه الطلبة بسيناريو واقعي، ويسألون أسئلة مثل: ماذا أعرف عن هذه المشكلة؟ ماذا يجب أن أعرف حتى أتمكن من وصف المشكلة؟ ما هي المصادر التي أستطيع استخدامها لتحديد حل مقترح أو فرضية ما؟ وبالتالي يتم تحديد المشكلة بحيث تتحول الى معلومة جديدة تم فهمها.
- الثانية: الوصول الى المعلومات وتقييمها، عندما يحدد الطلبة المشكلة وفقا للتساؤلات في المرحلة الأولى قد يصلون إلى معلومات من مصادر متنوعة إذ أن إحدى مكونات المشكلة هو تقييم المصدر من حيث مدى تداوله ودقته. وبالتالي تتلخص المرحلة الثانية بتقييم المصدر المستخدم لحل المشكلة.
- الثالثة: البناء والأداء، في هذه المرحلة يبني الطلبة حلا للمشكلة من خلال إعادة تنظيم المعلومات بطرق جديدة.
هذا وقد تناول العديد من المنظرين والفلاسفة والكتاب والباحثين في مجال العلوم التربوية إستراتيجية حل المشكلات ضمن أهم الاستراتيجيات التعليمية والتي كان لها أثر إيجابي في الرفع من التحصيل العلمي وتنمية التفكير وكثير من المتغيرات الأخرى لدى الطلبة وخاصة في مادتي الرياضيات والعلوم. ويمكن تبسيط أسلوب حل المشكلة كما ورد في (عبيدات وأبو السميد، 2009، 131) بما يلي:
- وضع الطلبة أمام المشكلة كما وردت في الكتاب المدرسي.
- تقديم المشكلة للطالب على أنها مشكلة واقعية حياتية.
- يحدد الطلبة إجراءات حل المشكلة والمعلومات التي يحتاجون إليها.
- يطبق الطلبة إجراءات الحل من خلال عملهم في مجموعات تعاونية.
مشكلة مقترحة:
المطلوب إيجاد طول عمود كهربائي لأقرب متر مربوط من رأسه تماما حبل غير قابل للمط طوله (100) متر، جزء من الحبل مطوي على الأرض بطريقتين مختلفتين.
يناقش المعلم هذه المشكلة مع الطلبة ويطلب منهم ذكر الحقائق التي يعرفونها حول المشكلة المطروحة.
ذكر الطلبة لبعض الحقائق التي يعرفونها مثل:
- الأفكار والحلول المقترحة.
- إحضار مقياس بالمتربات طوله يتجاوز 100 متر.
- علاقة المشكلة بموضوع دراسي معين.
- الحقائق المعروفة حول الموضوع المرتبط بالمشكلة.
- الحبل المربوط من رأس العمود الكهربائي والمتدلي على الأرض طوله 100 متر يمكن الاستفادة منه في حساب طول العمود.
- المشكلة لها علاقة بموضوع مبرهنة فيثاغورث.
الحقائق التي طرحها الطلبة مهمة وأساسية لحل المشكلة ولكن كيف يتم استثمارها في حل المشكلة؟ المعلم لا يتدخل في كيفية الاستخدام بل يترك للطلبة اكتشاف كيفية استثمارها في حل المشكلة.
المعلومات التي يحتاج إليها الطلبة لحل المشكلة (كيف يتم الاستفادة من الحقائق المطروحة من قبل الطلبة؟
يقود المعلم نقاشا حول كيفية الاستفادة من الحقائق المطروحة من خلال تفصيل المشكلة إلى أسئلة يطلب من الطلبة ضرورة الإجابة عليها كما يلي:
- هل يمكن الاستفادة من طول الحبل المتدلي على الأرض (المطوي على الأرض) لحساب طول العمود بشكل مباشر؟
- ما نص مبرهنة فيثاغورث؟
- هل يمكن اعتبار طول الحبل المربوط من رأس العمود والمتدلي على الأرض وتر في مثلث قائم؟
من خلال انهماك الطلبة في التفكير على إجابة الأسئلة المطروحة في النقاش الذي قاده المعلم يكونون بهذا قد قطعوا شوطا كبيرا في كيفية التعامل مع حل المشكلة.
خطة العمل:
يطلب المعلم من الطلبة مقترحات حول كيفية الحصول على إجابة الأسئلة المسبقة.
- استخدام المقياس المدرج بالمتر لقياس الجزء المتبقي من الحبل (المطوي على الأرض).
- الرجوع للكتاب المدرسي ومراجعة نص مبرهنة فيثاغورث.
- تمثيل العمود الكهربائي بعصا صغيرة وربطها بخيط من أعلى بطول معلوم بالسنتمترات ومحاولة تكوين مثلث قائم وتطبيق مبرهنة فيثاغورث.
بعد أن يتأكد المعلم بأن الطلبة قد أجابوا على الأسئلة يساعدهم في تنظيم المعلومات والإجابات في جدول كالتالي:
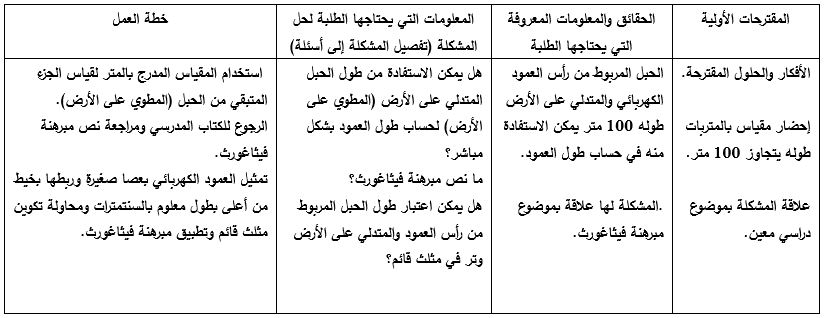
يستطيع الطلبة إضافة أية معلومات وحقائق وأفكار في الجدول.
كيف تنفيذ خطة العمل؟
لأن حل المشكلة في الأساس عملية تعاونية شارك الجميع في وضع خطة عملها، يمكن بدأ التنفيذ باستخدام أسلوب عمل المجموعات.
- يوزع الصف إلى مجموعات.
- تختار كل مجموعة مهمة معينة (إنجاز حل المشكلة بالطريقة المباشرة المتمثل بقياس الجزء المطوي على الأرض بعد تثبيت الحبل أسفل العمود تماما وقياس الجزء المتبقي، أنشطة العصا الصغيرة ومحاكاة العمود بمثلثات قائمة وحساب القياسات، تلخيص أفكار مبرهنة فيثاغورث…).
- تحديد فترة زمنية لإنجاز خطة العمل.
- تبادل الإنجازات كل مجموعة بالطريقة المناسبة.
- عرض النتائج وتحليلها وتقويمها.
نموذج ويتلي Wheatley: التعلم المتمركز حول المشكلة
صمم هذا النموذج جريسون ويتلي Wheatley,1991)) والذي يُعد من أكبر مناصري البنائية الحديثة، ويعبر هذا النموذج عن أفكار النظرية البنائية في تدريس الرياضيات والعلوم. ويرى ويتلي: أن الطالب في هذا النموذج (الإستراتيجية) يصنع له فهما ذا معنى من خلال مشكلات تقدم له؛ فيعمل تعاونيا مع زملائه على إيجاد الحلول لتلك المشكلات. (زيتون، 2007، 459). ويشير (علوان وآخرون، 2014، 259) بأنه من النماذج التي استخدمت في تدريس المفاهيم من خلال تطعيمه بالاستراتيجيات التعاونية داخل الصف الدراسي وفيه يختار المعلم مهمات على شكل مشكلات علمية أو أسئلة، ويقسم الطلبة على شكل مجموعات صغيرة وإثارة الدافعية لديهم نحو حل المشكلات أو الإجابة على الأسئلة المطروحة على المجاميع من خلال جلسة حوار داخل المجموعات الصغيرة، ويكون دور المعلم موجه ومساعد للطلبة في الوصول الى حل المشكلة أو حل الأسئلة المطروحة في المهمة.
خطوات نموذج ويتلي Wheatley:
يتضمن نموذج ويتلي Wheatley ثلاث مراحل دائرية نلخصها بالاستفادة من (علوان وآخرون، 2014، 259) كما يلي:
- الأولى: مرحلة المهام، وفيها يتم كتابة المهمة أو المهام التعليمية ويفضل أن تكون على شكل مشكلة تعليمية أو أسئلة يتطلب الإجابة عليها للوصول لمفهوم معين أو تعميم أو نظرية.
- الثانية: مرحلة المجموعات المتعاونة، وفيها يتم إنجاز الطلبة للمهام المقدمة في المرحلة الأولى ضمن مجموعات صغيرة حيث تعمل كل مجموعة في إطار أعضائها في المناقشة وتبادل الآراء للوصول إلى إنجاز المهمة.
- الثالثة: مرحلة المشاركة، بعد إنجاز المهمة ضمن إطار المجموعة الواحدة تتحول كل المجموعات الصغيرة إلى مجموعة واحدة وتقدم النتائج للمناقشة العامة ويتدخل المعلم لبلورة وتعميق الفهم العلمي السليم للمشكلة أو الأسئلة المطروحة في مرحلة المهمات.
كيف تنفذ نموذج ويتلي بمراحله في موضوع ما:
الموضوع: مساحة متوازي الأضلاع.
المهمة: إيجاد صيغة عامة لحساب مساحة شكل متوازي الأضلاع.
يمهد المعلم للمهمة بالتذكير بمساحة المستطيل، ويعطي الطلبة تلميحات حول كيفية إيجاد مساحة متوازي الأضلاع بالاستفادة من مساحة المستطيل. وفي نهاية التمهيد يطرح عليهم المهمة المتمثلة بإيجاد صيغة عامة لحساب مساحة شكل متوازي الأضلاع.
المجموعات الصغيرة: بعد التمهيد وعرض المهمة على الطلبة، يقسم المعلم الطلبة إلى مجموعات صغيرة بما يتوافق مع الإمكانيات المتاحة كبيئة الصف من جهة، ورأي المنظرين والفلاسفة في مجال التعليم فيما يخص معايير التعلم ضمن المجموعات الصغيرة. ويوزع عليهم أوراق العمل المعدة سلفا والتي من خلالها يستطيع التوصل إلى إنجاز المهمة بالتدرج (حساب مساحات متوازيات أضلاع مرسومة في ورقة مربعات الوحدة كأن يستخدم القص واللصق في تحويل متوازي الأضلاع إلى مستطيل مكافئ وحساب مساحته)، ومن ثم المرور على المجموعات ومراقبة التقدم في إنجاز النشاط (أوراق العمل)، ويحثهم على مناقشة الاستنتاجات والنتائج التي توصلوا إليها فيما يخص إنجاز المهمة المطروحة وتلخيصها استعدادا للمناقشة العامة.
المشاركة: بعد تأكد المعلم من أن كل مجموعة قد وصلت إلى أفكار تخدم إنجاز المهمة المطروحة يبدأ مع الطلبة بمرحلة المشاركة بجعلهم مجموعة واحدة كل مجموعة تطرح ما توصلت إليه من أفكار واستنتاجات ونتائج حول المهمة، ومن ثم يفتح نقاشا عاما معهم جميعا من خلال تطبيق الصيغة التي توصلت إليه كل مجموعة صغيرة ومدى صلاحيتها لحساب مساحة أي متوازي أضلاع حتى بلورة وكتابة الصيغة العامة.
نموذج شكل V:
على الرغم أن نموذج شكل V لم ينشأ ضمن سياق النظرية البنائية حيث أن مطوره (جوين) من أتباع نظرية التعلم ذي المعنى وبالتالي فإن النموذج ينتمي فكريا إلى نظرية التعلم ذي المعنى، إلا أن بعضا من منظري البنائية بينوا استخدامه في التدريس كونه يجسد بعض الأفكار الرئيسية في فلسفة العلم التي تؤكد على التفاعل النشط بين جانبي العلم ” الجانب المفاهيمي التفكيري والجانب الإجرائي أو ألعملياتي”، وبهذا يعتبر جوين Gowin صاحب الفضل في إنشاء خريطة أو نموذج شكل V وتطويره في نهاية السبعينات من القرن الماضي (1977) في ضوء أفكار البنائيين. كونه إستراتيجية توجه الطالب المتعلم لحل مشكلة أو فهم طريقة، كما أنه أداة تعليمية توضح التفاعل بين البناء المفاهيمي لفرع من فروع المعرفة والبناء المنهجي العملياتي له وبالتالي يساعد المتعلم على فهم المعرفة وفهم طرق بناء المعرفة. وقد لخص (عبيد، 2004، 160) نموذج شكل V بأنه مخطط مفاهيمي على شكل الحرف الانجليزي V وهو ذو بعدين أو جانبين: أحد الجانبين يخص المفاهيم والعلاقات (القوانين، المبادئ، النظريات) الخاصة بموضوع مستهدف بقصد تعلمه، والجانب الآخر يختص بالأعمال الإجرائية المتوقع أن يقع بها المتعلم، وتسبقها المتطلبات المعرفية المسبقة أي ما ينبغي أن يعرفه المتعلم كخلفية يبني عليها أو يربط بها المعلومات الجديدة لتكوين بنية معرفية أكثر ارتقاء من بنيته المعرفية السابقة. ويشمل التخطيط بشكل V ما يلزم للشرح أو الاستعمال من أدوات وأنشطة يقوم بها الطلبة للمساعدة في بناء أو إعادة تنظيم بنيته المعرفية سواء كان بناء ذاتيا وفقا لأفكار النظرية البنائية، أو بتوافق تكاملي بمعاونة المعلم وفقا لأفكار نظرية أوزبل.
لقد اقترح Gowin خمسة أسئلة توضح نموذج شكل V وهي (زيتون، 2007، 537):
- الأول: ما هو السؤال الإخباري؟
- الثاني: ما المفاهيم (الأساسية) المفتاحية؟
- الثالث: ما طرق الاستقصاء (الالتزامات الإجرائية) المستخدمة؟
- الرابع: ما المعرفة (الدعاوي المعرفية) الأساسية المدعاة؟
- الخامس: ما القيمة المدعاة؟
مكونات نموذج شكل V:
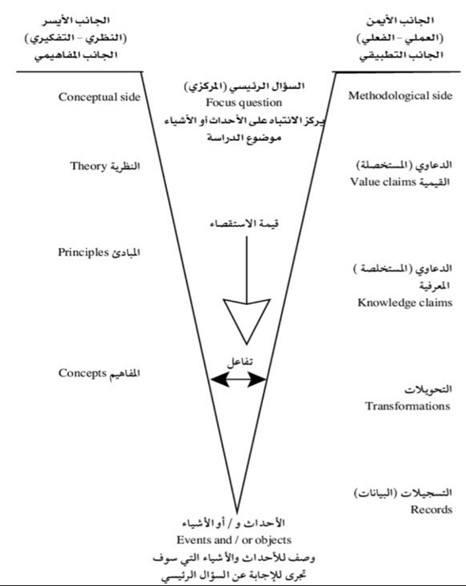
يوضح الشكل أعلاه مكونات نموذج شكل V حسب اقتراحات Gowin وافتراضاته المتضمنة العناصر المفاهيمية والمنهجية التي تتفاعل معا ويتم من خلالها إنتاج المعرفة الجديدة وتكوينها أي أن: نموذج شكل V يؤكد على ربط الجانبين العملي – التجريبي والمعرفي فيما يتصل مع الحوادث والظواهر، مما يعني بأن الجانب العملي يكتسب معنى عندما يرتبط بالبنية المعرفية السابقة لدى المتعلم. وفي قاعدة نموذج شكل V عند التقاء ضلعيه يوضع الأحداث والأشياء (ظواهر الاهتمام) التي يبدأ المتعلم بملاحظتها كونها نقطة البداية في إنتاج المعرفة وتكوينها، وفي ضوء ملاحظة المتعلم تنشأ لديه أسئلة يريد معرفة الإجابة عنها، وبعد الملاحظة يتم تسجيلها ومن ثم عرضها وتصنيفها بطريقة تساعده على الإجابة، ومن ثم يخرج بالنتائج التي تسمى بالدعاوي (متطلبات) المعرفية وهذا ما يمثله الجانب أو البعد أو الضلع المنهجي (التطبيقي)، وغالبا ما تتم الملاحظة في إطار مفاهيمي أي في إطار المبادئ العلمية والنظريات والفلسفات والتي تمثل الجانب أو البعد أو الضلع المفاهيمي حيث تكون المبادئ أقرب إلى الأشياء والأحداث التي تلاحظ، ثم النظريات باعتبارها أشمل من المبادئ، ومن ثم الفلسفات باعتبارها أشمل من النظريات. وبالتالي يتضمن نموذج شكل V تفاعلا بين الجانبين أو الضلعين المفاهيمي (التفكيري) والتجريبي (التطبيقي) مما يؤكد ارتباط الجوانب النظرية (التفكيرية) بالجوانب العملية التطبيقية. ويلخص (الدليمي، 2014، 104) مكونات نموذج شكل V اللازمة لفهم طبيعة المعرفة وبنائها في أي فرع من فروع المعرفة كما يلي:
- الجانب الأيسر: وهو الجانب المفاهيمي التفكيري، ويشتمل على المفاهيم والمبادئ والنظريات التي يتضمنها الدرس، ويشير هذا الجانب إلى تسلسل وتنظيم هرمي يتدرج من العام الى البسيط.
- الجانب الأيمن: ويعرف بالجانب الإجرائي أو العملياتي أو المتطلبات المنهجية ويشتمل على تدوين الملاحظات وتحويلاتها والمتطلبات المعرفية ذات القيمة، بحيث يتم ترتيباتها وصياغتها بشكل له معنى. ويوجد في بؤرة الشكل V الأحداث والأشياء، ويحدث تفاعل بين الجانبين الأيمن والأيسر للشكل من خلال السؤال الرئيسي الذي يقع في قمة الشكل V بين الجانبين المفاهيمي والإجرائي. علما بأن المكونات السابقة تمثل العناصر الأساسية في نظرية المعرفة طبقا لترتيبها في خريطة الشكل V.
خطوات التدريس وفق نموذج الشكل V:
التدريس وفق نموذج الشكل V بما يتوافق مع أفكار البنائية يتم وفق الخطوات التالية: (زيتون، 2007، 542).
- الخطوة الأولى: وتتمثل بصياغة السؤال البحثي (الرئيسي)، وفي هذه الخطوة يقدم المعلم موضوع الدرس بعد الإعداد للأنشطة التعليمية المناسبة، ويقسم الطلاب إلى مجموعات تعاونية، ويجرهم إلى طرح أفكار متنوعة من خلال الحوار والمناقشة وتهذيب الأفكار وصقلها وتوجيهها والتي من خلالها يتم طرح سؤال بحثي حول موضوع الدرس بصيغته النهائية.
- الخطوة الثانية: تحديد المعلومات السابقة اللازمة والتي من خلالها يتمكن الطلبة من التوصل إلى الإجابة على السؤال البحثي.
- الخطوة الثالثة: تحديد الجانب (الأيسر) المفاهيمي (التفكيري) لشكل V، وفي هذه الخطوة تقوم كل مجموعة تعاونية صغيرة من خلال الحوار والمناقشة وتبادل الأفكار وتلاقحها بتحديد المفاهيم والمبادئ والنظريات ذات العلاقة باستقصاء السؤال الرئيسي وبحثه.
- الخطوة الرابعة: بناء الجانب الأيمن التطبيقي العملي لنموذج شكل V، ويتم ذلك من خلال قيام الطالب بتحديد مكونات هذا الجانب التطبيقي بنفسه أولا، ومن ثم الحوار والمناقشة بين أفراد المجموعة التعاونية الواحدة ثانيا. ويتم تحديد مكونات الجانب التطبيقي كما يلي:
- التسجيلات: وتتضمن جمع البيانات وتسجيلها عن الأحداث.
- التحويلات: وفيها يتم عمل جداول إحصائية أو رسومات بيانية لكي يصبح للبيانات التي تم جمعها معنى.
- الدعاوي (المتطلبات) المعرفية يتم استخلاصها أو استنتاجها من التحويلات السابقة.
- الدعاوي المستخلصة (القيمية): بتحديد الدعاوي المستخلصة والتي تتداخل مع الدعاوي المتطلبة ولا تنفصل عن بعضها. يتكون لدى كل مجموعة تعاونية من الطلاب خريطة لنموذج شكل V بعد أن تم بناؤها من قبل كل مجموعة تعاونية. ومن ثم يتم الامتداد لخطوة بنائية أخرى من خلال المشاركة وفقا لنموذج ويتلي المتعلق بالتعلم المتمركز حول المشكلة، وعليه تقوم كل مجموعة تعاونية بعرض خريطة شكل V التي قامت ببنائها على بقية المجموعات التعاونية الأخرى، ومن ثم تدور مناقشات جماعية حول خرائط الشكل V جميعها تحت إشراف المعلم وتوجيهه وإدارته.
مثال تطبيقي: استخدام نموذج شكل V في إيجاد مساحة المثلث
الهدف: إيجاد مساحة المثلث باستخدام القانون: م = القاعدة × الارتفاع.
الأدوات التعليمية:
- لوحة مربعات شبكية.
- أوراق عمل للطلبة.
- أوراق مربعات مرسوم عليها عدة أشكال لمربعات ومستطيلات موضحا عليها قطر (القطر يقسم كلا من المربع والمستطيل إلى مثلثين).
- تمارين يقوم بحلها الطلبة.
السير في الدرس:
بناء خريطة الشكل V وفق الخطوات التالية:
- نرسم الشكل V.
- نمد الشكل V من الجانبين الأيمن والأيسر بخطين نضع في قمة الشكل الفتحة المحاذية لامتداد الخطين السؤال الرئيسي: ” كيف يمكن حساب مساحة المثلث؟”
- على يمين الشكل V فوق الخط الممتد نضع الجانب المفاهيمي وتحته مباشرة نكتب الجوانب المفاهيمية والمتمثلة ب: تعريف المثلث، (مساحة المستطيل = الطول × العرض) قانون سبق للطالب معرفته، قطر المستطيل خاصية سابقة، كيف أن القطر يقسمه إلى مثلثين، ارتفاع المستطيل، قاعدة المستطيل.
- على يسار الشكل V فوق الخط الممتد نصع الجانب الإجرائي وتحته نكتب الجوانب الإجرائية والمتمثلة ب: المطلوب (المعرفة الجديدة) إيجاد مساحة المثلث بمعرفة قانون مساحة المستطيل والتحقق باستخدام ورقة مربعات، ومن ثم التعبير بالرموز عن المطلوب: مساحة المثلث= مساحة المستطيل= (الطول × العرض) = القاعدة × الارتفاع. ومن ثم يحل الطلبة أمثلة متنوعة ويربطونها بأمثلة حياتية كحساب مساحة نصف أرضية الفصل.
- في آخر الشكل V (أسفله): يتم توضيح الأدوات التي يتم استخدامها والأعمال التي يتوجب على الطلبة القيام بها والمتمثلة ب: لوحة مربعات، شفافيات يشرح عليها المعلم، أوراق عمل يعمل عليها الطلاب، مقص لقص المستطيل من القطر ليتضح للطلبة بأن القطر يقسم المستطيل إلى مثلثين متطابقين.
- أنشطة يقوم بها الطلبة والمتمثلة ب: محاولة البرهنة ويكتبها الطلبة بأنفسهم، ويتحققون من ذلك حسابيا وعدديا لحالات خاصة مرسومة أو يرسمونها بأنفسهم، وحل عدد من التمارين نظريا.
- أنشطة يقوم بها المعلم والمتمثلة ب: التقويم من خلال تقديم تدريبات وتمارين تطبيقية مثل: أوجد مساحة مثلث قاعدته 4 سم وارتفاعه 2 سم؟، إعادة تلخيص الدرس، إعطاء برهان منطقي لمساحة المثلث بناء على مساحة المستطيل، وإعطاء واجب منزلي.
المراجع:
إبراهيم، بسام، (2009). التعلم المبني على المشكلات الحياتية وتنمية التفكير، دار المسيرة للنشر، عمان- الأردن.
الدليمي، عصام حسن، (2014). النظرية البنائية وتطبيقاتها التربوية، دار صفاء للنشر والتوزيع، عمان- الأردن.
زيتون، عايش محمود، (2007). النظرية البنائية واستراتيجيات تدريس العلوم، دار الشروق للنشر والتوزيع، عمان- الأردن.
عبيدات، ذوقان وأبو السميد، سهيلة، (2009). استراتيجيات التدريس في القرن الحادي والعشرين دليل المعلم والمشرف التربوي، ديبونو للطباعة والنشر والتوزيع- عمان- الأردن.
عبد الحميد، جابر، (1999). استراتيجيات التدريس والتعليم، دار الفكر العربي، القاهرة.
عبيد، وليم، (2004). تعليم الرياضيات لجميع الأطفال في ضوء متطلبات المعايير وثقافة التفكير، دار المسيرة للنشر والتوزيع، عمان- الأردن.
علوان، يوسف ومحمد، يوسف وسعد، أحمد، (2014). المفاهيم العلمية واستراتيجيات تعليمها، دار الكتب العلمية- بغداد- العراق.
 تعليم جديد أخبار و أفكار تقنيات التعليم
تعليم جديد أخبار و أفكار تقنيات التعليم







مقال رائع جداً. سلمت دكتور