تعتبر مادة الرياضيات من أهم المواد الدراسية التي تحظى بعناية خاصة في جميع الأوساط التربوية في مختلف دول العالم، لذلك لجأت بعض المنظمات التربوية الدولية لإجراء دراسات دولية تقارن بين أداء الطلاب في التحصيل ومدى امتلاكهم لأساسيات ومهارات الرياضيات، فنشأت من ذلك العديد من المسابقات والدراسات الدولية مثل: (البرنامج الدولي لتقييم الطلبة PISA) تحت إشراف منظمة التعاون الاقتصادي والتنمية (OECD)، و(الاتجاهات العالمية في التحصيل الدراسي للرياضيات والعلوم TIMSS) تحت إشراف المنظمة الدولية لتقويم التحصيل التربوي (IEA)، وتحرص المملكة العربية السعودية على المشاركة في هذه الاختبارات الدولية للوصول إلى مصاف الدول المتقدمة علمياً وفكرياً والحصول على نتائج أفضل للطلبة.

وبعد قراءة نتائج اختبار (2019،TIMSS ) وإجراء دراسات تقويمية كل أربعة أعوام لطلبة الصفين الرابع والثامن (الثاني المتوسط)، في عدد من الدول المشاركة، ومقارنة نتائج أداء الطلبة بناء على عدة بيانات مؤثرة، كالبيئة التعليمية من معلم ومنهج وتجهيزات مدرسية وتقنية وبيئة منزلية للوصول إلى تعليم أفضل،  ظهرت رؤى مختلفة لعدة جهات حكومية وتباينات في عملية التحليل، ومن أهم هذه الجهات وزارة التعليم كجهة تنفيذية تعمل على تدريب وتأهيل الطلبة للاختبارات الدولية، والتي رأت أن النتائج تعتبر إنجازاً بالنسبة للدورتين السابقتين عام 2015-2011 م، وحصول المملكة على المركز (53) من (58) دولة مشاركة، والمركز ما قبل الأخير في دولة مجموعة العشرين للصف الرابع، كما حصلت المملكة على المركز (36) من (38) دولة مشاركة للصف الثامن.

هذه الرؤية الإيجابية لوزارة التعليم كانت بناء على التقدم الذي حققته المملكة من بين أعلى الدول كدورتين متتاليتين وثاني دولة من مجموعة العشرين في تحسين النتائج، كما رأى ذلك وزير التعليم السابق الأستاذ حمد ال الشيخ، وبالتالي تم النظر في كافة البيانات التي تم جمعها من الاختبارات الدولية، والعمل على تطوير التعليم في ضوئها،  فقامت الوزارة على زيادة عدد الحصص، وإصدار نظام التقويم الدراسي الجديد (ثلاث فصول دراسية بدلاً من فصلين)، وإطلاق الاختبارات المحاكية للاختبارات الدولية، لقياس مستوى الطلبة وتجويد نتائج التعلم في جميع مدارس التعليم العام، بينما ترى هيئة تقويم التعليم والتدريب أن هذه النتائج غير موفقة، وأصدرت تقريرا بذلك، و أن نسبة كبيرة من طلبة المملكة تنقصهم المهارات والمعارف الأساسية للرياضيات، وجاءت هذه الرؤية كنظرة سلبية لنتيجة الاختبار، لأن العديد من الطلبة لم يحققوا المعايير الدولية المنخفضة، وهذا يدل على النقص الشديد وانخفاضها لدورتين أو ثلاث متتاليتين مما يدل على انخفاض جودة التعليم.

وبالتالي تعتبر جودة التعليم من أهم القضايا التي لابد أن تسعى منظومة التعليم لتحقيقها في ضوء معايير وآليات مقننة وأساسية تشمل المناهج التعليمية، والأطر التربوية والإدارية، والبنية التحتية واستخدام التقنية، والاهتمام بالطالب والبيئة من حوله، وقد أكد التربويين  أن التحسين لابد أن يشمل الجميع من طلبة عاديين ومتفوقين، لأن الاهتمام بالطلاب ذوي الأداء المنخفض يساعد في حصول الدولة على نتيجة أفضل، من خلال تقارب النتائج لجميع الطلاب ، والحصول على تحسين متوسط الإنجاز للدولة بطريقة أكثر عمق واستدامة من الأنشطة المركزة على الطلبة المتفوقين وإهمال البقية.

ومن أهم طرق التدريس التي أثبتت فاعليتها في تحقيق التدريس الفعال، والمعالجات المتنوعة، وتطورت مع تطور التعليم لتحقيق النمو الشامل للمتعلم، وعدم الاقتصار على النمو المعرفي له، طريقة التعلم القائم على الإتقان، تسعى هذه الطريقة لتنظيم التعلم، ووضع أهداف محددة له حتى يتم التحقق من إتقان المادة التعليمية والوصول إلى أعلى درجات الإتقان، والتي تعتبر كمدخل من مداخل تدريس أكثر عمقاً في الرياضيات وهو مدخل CPA اختصار (CONCRETE PICTORIAL ABSTRACT )، وتعني مدخل (المحسوس وشبه المحسوس والمجرد)، والتي تستند إلى نظرية التعلم لدى العالم برونر(BRUNER)، وهي من النظريات المعرفية البنائية، التي تستند على مبادئ تتعلق بعمليات التعليم والتعلم، كتشجيع المتعلمين على تنظيم المعرفة واكتسابها، وتفسير المواقف نتيجة اكتساب الخبرات، واكتشاف حلول للمشكلات، وتنمية المعارف الجديدة واكتسابها، وبالتالي تتناول طريقة تدريس عميقة هدفها الوصول إلى الإتقان.

ومن أبرز الدول التي تعتمد على هذا النهج في عملية التدريس هي دولة سنغافورة، الحاصلة على المراكز الأولى في كل مرة في الاختبارات الدولية، فقد تميزت باستخدام إتقان التعلم في جميع مناهجها وفي الرياضيات على وجه الخصوص، فيها يتم تقديم المفاهيم بشكل يراعي مراحل النمو المعرفي لدى الأطفال، ولذلك فإن الاستعداد للتعلم ليس ناتجاً فقط عن النضج، ولكن يهتم بتنظيم البناء المعرفي للمادة المتعلمة بطريقة معينة تمكن المتعلم من أن يستوعبها مهما كان عمره (Supandi&Waluya,2018).

لذا فإن اعتماد سنغافورة لهذه الاستراتيجية انطلاقاً من رغبتها في تقليل الإحباط في التعلم عند المتعلمين وخصوصاً طلاب المرحلة الابتدائية  الذين لايزالون في المرحلة المعرفية للتعلم المحسوس، وأن يكونوا أكثر قدرة على تعميق فهمهم باستخدام كلماتهم الخاصة، وأكثر ثقة في التبريرات الرياضية، والتفسيرات التي اعتاد المتعلمون على الإخبار بها وكتابتها في المرحلة المحسوسة، وهذا ينمي قدرتهم على التفكير بشكل إبداعي في حل المشكلات، كما أن لها تأثيرا إيجابيا كبيرا على فهم الطلاب المفاهيمي ونتائج التعليم ( التمثيل الرياضي) للمتعلمين حيث أظهرت نتائج البحث الذي أجراها (Witzel,2003) أن  CPA تساعد الأطفال على التعلم و مواجهة الصعوبات الرياضية وعلى ارتكاب أخطاء أقل عند محاولة حل مشاكل أكبر، كما تعزز تصرفات الطلاب واتجاهاتهم نحو التعلم في الفصل الدراسي، وتعمل على توفير فرصة لتحسين فهم الرياضيات، من خلال تسلسل مراحل التعلم الثلاث كدائرة هرمية تبدأ باستخدام الأشياء المحسوسة، ثم عمل تمثيلا تصويريا للأشياء المحسوسة، وفي إنهاء عمل الطلاب في التدوين المجرد. وبتمرير هذه المراحل الثلاث من التعلم، من المتوقع أن يفهم الطالب المفاهيم الرياضية بشكل واضح وصحيح، ويشعر بالفوائد فور تعلم الرياضيات. (Putri, 2015 ؛Hafiziani,2015).

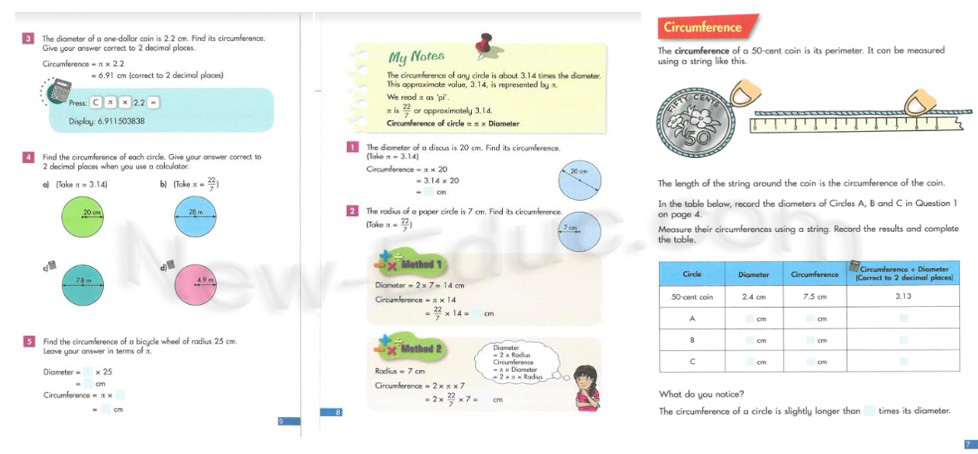
شكل.1 مراحل التعلم الثلاث في CPA  (McCourt, 2019)

ويؤكد (McCourt, 2019) أن مدخل CPA يعمل على  توصيل الفكرة الجديدة بطريقة تمكن جميع التلاميذ من تكوين معنى وإحساس الفكرة، بحيث سيستخدم المعلم مجموعة من النماذج والاستعارات والأمثلة للسماح لجميع التلاميذ برؤية كيفية ارتباط الفكرة الجديدة بما يعرفونه بالفعل وكيفية اتصال التمثيلات المختلفة ببعضها البعض.

شكل.2 (نماذج من كتاب الرياضيات السنغافوري (6B)

إن طريقة التعلم من أجل الإتقان ليست بجديدة، حيث يعد التعلم من أجل الإتقان من المفاهيم القديمة والحديثة نسبيا في مجال التربية، فقد ظهر خلال القرن العشرين مع كتابات عدد من المربين من أمثال ديوي وغيره، وهو يعني نوعا من أنواع التعلم الإنساني الذي نحاول فيه تأكيد إتقان المتعلم لمجموعة محددة من الأهداف السلوكية (الخليفة ومطاوع،2015)، وكما أن جذورها التاريخية تعود إلى العشرينيات من القرن الماضي، حيث كانت هناك محاولتان لتقديم تعليم متميز قائم على التعلم الإتقاني إحداهما خطة Winnetka عام 1922 م ، والأخرى طريقة Morrison عام 1929 م، إلا أن فكرة التعلم الإتقاني قد اندثرت بعد هاتين المحاولتين لنقص التكنولوجيا اللازمة لدعمهما، من ناحية، ومواجهة بعض مشكلات التطبيق في التعليم المدرسي، من ناحية أخرى. وقد عاودت هذه الفكرة الظهور مرة أخرى في أواخر الخمسينيات وبداية الستينيات من القرن الماضي نتيجة ظهور التعليم البرنامجي على يد سكنرSkinner.(الكسباني،2007)

كما أن ظهور التعلم من أجل الاتقان في اليونان القديمة، على يد أرسطو أحد تلاميذ أفلاطون، والذي كرس نفسه لتطوير إحدى النماذج المعرفية، التي يرى فيها أن المعلم يكون على علم بما يتعلمه طلابه، وأين يصلون في تعلمهم، ويصحح لهم مفاهيمهم الخاطئة التي تكونت لديهم أثناء التعلم، وهذا الأساس الثابت للتعلم من أجل الإتقان، بحيث يفهم الطالب الموضوعات بمزيد من العمق ويصبح أكثر ثقة بقدراته الرياضية. وبعد ذلك ظهرت حركة إتقان الرياضيات في المدارس الابتدائية على يد كارلتون واشبورن لرفع مستوى التدريس، وظهر بلوم في منتصف العشرينات وطور نموذج كارلتون لتحسين أثر التعليم، فقام بجمع السمات الأساسية لنموذج الإتقان وأمضى جزءاً كبيراً من حياته في تحسين المواد التعليمية والتقييمية، وطرق وأساليب نشر هذا النموذج على نطاق واسع وبطريقة عملية، وكان يقوم دائماً باختبار مدى فعاليتها، إلى جانب أساليب التقدم المتكامل في مجال التكنولوجيا بغرض تحقيقها لتأثير أكبر، ويرى أنه يمكن لجميع التلاميذ أن يتعلموا بشكلٍ جيد عن طريق منحهم الوقت المناسب لذلك، والظروف الملائمة لجميع التلاميذ  كما يؤكد أنه إذا كان بمقدور المعلمين إتاحة الوقت المناسب لكل تلميذ للتعلم وتوفير الظروف الملائمة للتعلم لجميع التلاميذ، فإنه يمكن لكل تلميذ أن يتعلم بشكلٍ جيد (McCourt, 2019).

ويؤكد (McCourt, 2019) أن نموذج الإتقان والتمكن من التعليم هو دورة تعليمية مستجيبة يسعى فيها المعلم باستمرار إلى بناء المعرفة بنظام ما بمرور الوقت في رحلة مجدولة ومتماسكة بعناية، تؤدي إلى فهم أوسع وأكثر تعقيدًا لذلك التخصص وعلاقة الفرد بها. ويبحث المعلم باستمرار عن التغييرات في معرفة ومهارات وفهم التلميذ كمؤشرات للمعلم لاتخاذ بعض الإجراءات، بما في ذلك العمل بشكل مختلف عما كان عليه من قبل. يدرك المعلم ويؤمن تمامًا أن جميع التلاميذ يمكنهم أن يتعلموا جيدًا إذا كانت خياراتهم التربوية والتعليمية مدروسة بعناية وبراعة ودقه. يمكن لكل تلميذ تحت مسؤولية المعلم أن يكون ناجحًا. حيث يستخدم المعلم نهجًا للتشخيص والتحسين المستمر يعتمد على ما يعرفه ويفهمه التلميذ بدقه، وذلك بهدف مواصلة تطوير مخطط معرفتهم في إطار منطقي للحقيقة.

إن استخدام مدخل التعلم بالإتقان، وتوضيح طرق اكتساب الطلبة للمفاهيم والمعارف والمهارات في المناهج الدراسية وما تتضمنه الاختبارات الدولية، يمكّن من استثمار القدرات الكامنة للطلبة، وتوظيفها في تعلمهم، ليصبحوا متجاوبين مع متطلبات الثورة الصناعية الرابعة ومهارات القرن الحادي والعشرين، ووظائف المستقبل، والمشاركة في التنمية الوطنية والقدرة على المنافسة عالميا، من خلال تحسين مخرجات التعليم وأداء الأطر (الكوادر) البشرية، وتحقيق رؤية 2030م والتنمية الاقتصادية المستدامة.

المراجع:

الخليفة، حسن جعفر؛ مطاوع، ضياء الدين محمد (2015). استراتيجيات التدريس الفعال، الدمام: مكتبة المتنبي.

الكسباني، محمد السيد علي (2007). التدريس نماذج وتطبيقات في العلوم والرياضيات واللغة العربية والدراسات الاجتماعية، القاهرة: دار الفكر العربي.

McCourt, M (2019). Teaching for Mastery. Woodbridge: John Catt Education

Putri, H. E. (2015). The Influence of Concrete-Pictorial-Abstract (CPA) Approach to The Mathematical Representation Ability Achievement of the Pre-Service Teachers at Elementary School. International Journal of Education and Research, 3(6), 113-126.

Hafiziani. (2015). The influence of Concrete Pictorial Abstract (CPA) approach to the mathematical representation ability achievement of the pre-service teachers at elementary school. International Journal of Education and Research, 3(6), 113-126. Retrieved 3 April 2020  from http://ijern.com/journal/2015/June-2015/09.pdf.

Witzel, B. S.; Mercer, C. D. & Miller, M. D. (2003). Teaching algebra to students with learning difficulties: An investigation of an explicit instruction model. Learning Disabilities Research & Practice, 18(2), 121–131.

Supandi, S., Waluya, S. B., Suyitno, H., & Dewi, K. (2018). Think-Talk-Write Model for Improving Students’ Abilities in Mathematical Representation. International Journal of Instruction, 11(3), 77–90.