عبر الحضارات الإنسانية المتعاقبة، اهتم الإنسان بتعليم وتعلم الرياضيات لما يحتاج فهمها من إدراك لمفاهيمها وحقائقها وتعميماتها ولغتها، إضافة إلى استيعاب وتوظيف للعلاقات والأنماط الرياضية في المواقف الرياضية المختلفة والقدرة على تفسير وتبرير لإجراءات حلها والتنبؤ بحلول المواقف الرياضية والقدرة على التمثيلات الرياضية والربط بينها وترجمتها لفظيا وكتابيا؛ مما يستدعي التفكير (Zaitoun, 2003).
تعد الرياضيات من أهم العلوم التي أسهمت في تطور الحضارة الإنسانية، وقد ساعدت على فهم العلوم الطبيعية المختلفة كالفيزياء والفلك والإحصاء وغيرها من العلوم. فالرياضيات علم مبني على سلسلة من المفاهيم والحقائق والرموز، ولغة تجد من الصعب على من لا يلم بها أن يدرك ماهيتها، فهو علم أساسه التفكير الرياضي الذي يدعم الفهم بالعلاقات والأنماط والتمثيلات الرياضية وحل المشكلات الرياضية.
ولذا؛ فقد أولى التربويون أهمية خاصة لتعلم وتعلم الرياضيات، وتنطلق الرياضيات المدرسية كما يراها تيل المذكور في (Obida, 2016) من كونها تمثيل للعالم الواقعي الذي يواجه الطلبة في ثلاثة مستويات أو عوالم متكاملة ومتمايزة تتمثل في: عالم التجسيد المفاهيمي Conceptual-Embodied World ويتمحور في رؤية الأشياء وتأملها والإحساس بها ومن ثم تخيلها لبناء صورة ذهنية لها بإعطاء التعريفات وتوضيح خصائص الأشكال واكتشاف العلاقات الرياضية ووصفها. و عالم الإجراءات- الرمزية Perceptual- Symbolic World، وذلك بتوظيف اللغة الرياضية بما تحتويه من رموز وتعبيرات منطقية في بناء خوارزميات تدعم حل المشكلات الرياضية وتوظيف التمثيلات الرياضية لبناء نسق رياضي متين، وعالم البديهية- المنهجي Axiomatic- Formal World ويرتبط بتمييز البديهيات الرياضية وتوظيف منهجية البرهان الرياضي في بناء المعرفة الرياضية وتطويرها.
وتمثل الرياضيات المدرسية مجموعة من الأنشطة العقلية التي تعمل على بناء العديد من الأنماط الرياضية التي تساعد على حل المشكلات الرياضية كالتفسير الرياضي، والتصور الذهني، والتحليل الرياضي، والتركيب الرياضي والشرح الكتابي واللفظي الرياضي، ووضع الفرضيات واختبارها واتخاذ القرار والاستنتاج.
وللتفكير أهمية كبيرة فهو الهدف الأساس في التعليم والتعلم، حيث اهتمت النظريات التربويه الحديثة كالنظرية البنائية Constructivism Theory في التركيز على ما يدور في ذهن المتعلم، وعليه يرى العديد من التربويين أن المعرفة المتخصصة لن تصبح مهمة لجيل المستقبل، بل الأهمية في معاملتها ذهنيا من خلال آلية يطلق عليها ” تعليم التفكير”، كذلك اعتبار مهارة التفكير عملية ذهنية أدائية توظف في مجالات التعلم وفروع المعرفة المختلفة، حيث أصبحت في قمة أولويات النظم التربوية المتقدمة في العالم (Jarwan, 2008).
وقد أكدت وثيقة مبادئ ومعايير تعليم وتعلم الرياضيات Principles and Standards of Teaching and Learning Mathematics الصادرة عن المجلس القومي لمعلمي الرياضيات بالولايات المتحدة الأمريكية (National Council of Teachers of Mathematics) على التركيز على تنمية التفكير الرياضي لجميع الطلبة ولكافة فئاتهم العمرية في وثيقة (NCTM, 1989).
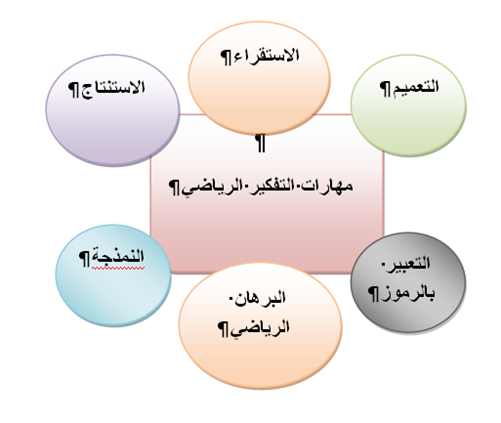
مهارات التفكير الرياضي
وقد أشار كرينجر Krienger المذكور في (Alzoebi, Rowaka & Shamot, 2018) بأن التفكير الجبري يعد من أهم أنواع التفكير الرياضي، حيث أن مهاراته توجد في كافة المراحل التعليمية للطالب. وللتفكير الجبري تعريفات متعددة، فقد عرفه ويل (Will, 2010) بأنه ” أحد أنماط التفكير أو الاستدلال الرياضي، يرتبط بعمليات عقلية يقوم بها الطالب لاستيعاب ووصف الأنماط والعلاقات الرياضية، واستنتاج علاقات رياضية جديدة حول الأعداد والعمليات والأشكال الرياضية، ويرتبط التفكير الجبري بتنمية مجموعة من المهارات لدى الطلبة منها: الاستدلال حول الأنماط الرياضية في الرسوم والأشكال الهندسية والأعداد والعمليات الحسابية، واستنتاج التعميمات الرياضية وتوظيفها، وتنمية الأداء العقلي فيما يرتبط بالعمليات على المقادير الجبرية، واستخدام التمثيلات الرياضية في وصف العلاقات الرياضية”. كما عرفه سيوي (Swee, 2004: 40) بأنه ” مجموعة الأنشطة والعمليات العقلية المرتبطة بالأنماط والعلاقات الرياضية، ودراسة الاقترانات، ويتضمن تنمية مجموعة من المهارات تتمثل في: التصنيف، والمقارنة، وتحديد الجزء من الكل، ووصف الأنماط الرياضية وبناء أنماط جديدة، وتحديد ووصف العلاقات الرياضية بصورة لفظية ورمزية، وتنمية الاستدلال الجبري، مع توظيف الأنشطة والعمليات والمهارات الرياضية المرتبطة بالمحتوى العلمي في حل المسائل الجبرية”.
يتكون التفكير الجبري من مكونين رئيسيين هما: أدوات التفكير الرياضي والأفكار الجبرية الأساسية، حيث أن أدوات التفكير الرياضي تشمل مهارات حل المسألة الرياضية والتي تتضمن استخدام استراتيجيات حل المسألة الرياضية واستخدام حلول متعددة ومهارات التمثيل الرياضي، والأفكار الجبرية التي تعبر عن محتوى المادة الدراسية ويتم اكتشافها من خلال اعتبار الجبر كحساب معمم والجبر كلغة للرياضيات والجبر كأداة الاقترانات والنمذجة. وأوضح اسيالا وآخرون (Asiala etal., 1996) أهمية تدريس الجبر في مراحل مبكرة، وضرورة التركيز على تنمية مهارات التفكير الجبري وتنمية المهارات الخوارزمية وحل المسائل الجبرية، خاصة المسائل اللفظية التي تدعم الطلبة في عمليات الترجمة والتمثيل الرياضي، كما أشار ألتون (Alton, 2003) إلى إمكانية تنمية مهارات التفكير الجبري في الصفوف الأولى بالتكامل بين مجال الأعداد والعمليات عليها ومجال الجبر والعلاقات.
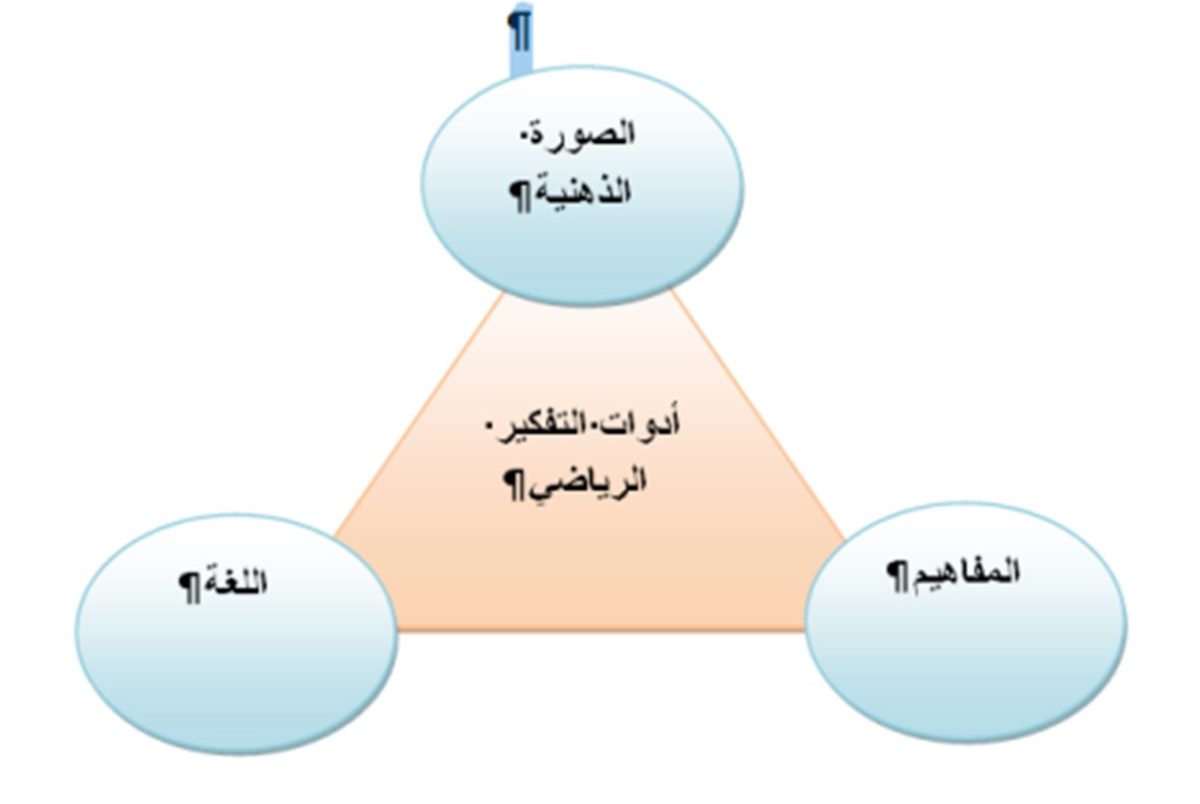
أدوات التفكير الرياضي
وقد أكد سميث وطومسون (Smith & Thompson, 2007) على أن دراسة الجبر تتطلب من الطالب معرفة الرموز الرياضية وقراءة التعبيرات والمقادير الجبرية واستخدام العلاقات والأنماط الرياضية في وصف المواقف الرياضية والقدرة على التمثيلات الرياضية وترجمتها لفظيا وكتابيا وحل المشكلات اللفظية والقدرة على ترجمتها إلى معادلات وحل الاقترانات وتمثيلها، وقد أشار المجلس القومي للبحوث National Research of Council (NRC) لأهمية تنمية مهارات التفكير الجبري عند الطلبة بما يتلاءم ومتطلبات القرن الحادي والعشرين (NRC, 2010).
المراجع:
Asiala, M.; Brown, A.; DeVries, D.; Dubinsky, E.; Matthews, D. & Thomas, K. (1996). A framework for research and curriculum development in undergraduate mathematics education. Research in Collegiate Mathematics Education, 2: 1-32.Jarwan, F. (2008). Teaching Thinking: Concepts and Applications, Edition 3, Amman: Dar Alfikr.Obida, N. (2016). The effect of using multiple mathematical representations in teaching mathematics in developing algebraic thinking skills, algorithmic skills, and solving algebraic problems among middle school students,ASEP Arab Studies in Education and Psychology 1(75), 117- 170
National Council of Teachers of Mathematics (NCTM) (1989). Principles and Standards for School Mathematics, Reston, VA: The Auther.
National Research Council (NRC) (2010). Assessing 21th Century Skills, Washington, DC: National Academics Press.
Smith, J.& Thompson, P. (2007). Quantitative Reasoning and the Developing of Algebric Reasoning , In J.J. Kaput, D. W. Carraher & M. L. Blanton (Eds.), Algebra in the early grades (pp. 95- 132), New York: Erlbaum.
Zaitoun, A. (2007). Constructivist Theory and Strategies for Teaching Science, First Edition, Amman: Dar al- shorouk.
Swee, F. (2004). Developing algebraic thinking in early grades: case study of the Singapore primary mathematics curriculum, The Mathematics Educator, 8(1), 39- 59.
Alzoebi, A., Rawaka, K. & Shamot, A. (2018). The Effect of An Instructional Strategy Based on Dubinsky’s Theory on the Development of Algebraic Mathematical Thinking Related to Functions, IUG Gournal of Education and Psychology Sciences, 26(2), 464- 486.Will, W. (2010). Algebraic thinking: a problem solving approach, in: Sparrow L., Kissane B.& Hurst C. (Eds.). Shaping the future of mathematics education: Proceedings of the 33rd annual conference of the Mathematics Education Research Group of Australasia, Fremantle: MERGA, 665- 672.
 تعليم جديد أخبار و أفكار تقنيات التعليم
تعليم جديد أخبار و أفكار تقنيات التعليم