“رُبّ خطأ أنفع للمتعلّم وللمعلّم من إجابة صحيحة”

تقديـــــم

لقد انبرى المختصّون في ديداكتيك الرّياضيات لتعميق النّظر في أخطاء المتعلّمين وإخراجها من الفصل إلى عالم البحث والاستقصاء. ولعلّ أوفى صورة تعكس اهتمامهم بتلك الأخطاء ما راكمته الدّراسات المختصّة من استنتاجات. فغدت شواهد على تحوّل عميق في فهمنا للخطأ حيث اتّفقت جميعُها على أنّ الأخطاء ليست جريدا من المصطلحات في علاقة بالمفاهيم المدرّسة بل أثر ناصع لنظام من الحدوسات والتّصورات توجّه تفكير المتعلّم. فصَوَابِيَّةُ توظيف الأخطاء أثناء التّمشي التّعلّمي التّعليمي تجد سندا في اعتبار الخطإ كاشف تصوّرات المتعلّمين وإوالياتهم الذّهنيّة عند مواجهة مهمّة رياضيّة محدّدة. فالأخطاء تلابس التّصوّرات وتعبّر عنها.

لكن الصّورة المثلى الّتي أنشأها المختصّون حول الخطإ، لم تكن بالصّفاء التّام لدى المدرّسين لأسباب متنوّعة أهمّها النّقص الحاصل في التّكوين: فالمدرّس يواجه صعوبات جمّة في هذا المجال. ويكون من المفيد التّدقيق في الأطر النظريّة والمرجعيّة للخطإ واقتراح تبعا لذلك سبلا ناجعة لاعتماده أثناء التّعلّمات.

 

Iـ الخطأ في ديداكتيك الرياضيات

Iـ1ـ مكانته

يرى Jean brun (2002) ⁽¹⁾ أنّ النّظرة إلى مكانة الخطإ قد تغيّرت حيث لم يَعُدْ الخطأ صِنْو العُطْل والعطب بل تحوّل إلى وسيلة للتّعلّم.

ويؤكدAlain Bouvier (1986) ⁽²⁾ أنّ إجابات التّلاميذ الخاطئة لا تأتي صدفة لأنّ التّأتّي الذّهني للمتعلّمين يشتغل وفق نظريـات (théorèmes) تكون غير واضحة بالنسبة إليهم وخاطئة بالنسبة إلى المدرّس لكن لها مكانة النّظريّة عندهم. وأنّ في تاريخ تطوّر الرّيـاضيات نجد ما يماثلها من ذلك مثلا أنّ Glaeser ـ عنـد دراسـته لقاعــدة العلامــات (la règle des signes) ـ تبيّن أنّ L. Carnot (1823-1723) ـ وهو رياضيّ مشهور في عصره ـ كان يعتقد أنّ  لأنّ البسط أكبر من المقام في الكسر الأوّل والعكس بالنسبة إلى الكسر الثّاني؟! وقد دعا Alain Bouvier إلى ضرورة أخذ هذه النظريات ـ التّلمذيّة بجديّة وفهمها لأنّ أخطاء المتعلّمين تُنبئنا:

– عن الكيفيّة الّتي يتعلّمون بها،

– عن التّعلّمات الّتي اقترحت عليهم،

– عن صعوباتهم الوجدانيّة تجاه الرّياضيات،

– عن وجود عوائق ذات طبيعة تعلّميّة،

– عَمَّ هو ضمني بين المدرّس والتّلميذ،

– عن معنى تعليم الرّياضيات.

Iـ2ـ الخطأ في النّماذج البيداغوجيّة

يقرّJ.P Astolfi (1997) ⁽³⁾ أنّ مكانة الخطإ هي دالّة تصوّرنا للنّموذج البيداغوجيّ المعتمد.  ففي النّموذج التّمريري حيث يُعْلى من شأن المعرفة على حساب المتعلّم. يُعتقد في اختصار عمل المدرّس شرحا وتبيينا حتّى تحصل عمليّة اكتساب المعرفة دون أخطاء. ويحتلّ الخطأ ـ داخل هذا النموذج ـ مكانة “الخطيئة”. فهو من مسؤولية المتعلّم لأنه لم يبذلْ مجهودا للتّكيف مع الوضعيّة التّعليميّة. وفي النّموذج السّلوكي الكلاسيكي، وإن اختلفت مكانة الخطإ عن النّموذج السّابق بأخذه في الحسبان، فإنّ الجهد عادة ما ينصبّ على تحاشيه من خلال هيكلة الوضعيّة التّعليميّة. ويردّ الخطأ هنا إلى سوء البرمجة وعدم قدرتها على التّكيّف مع مستوى المتعلّمين. فالخـطأ يـرادف “الـهفوة البرماجاتيّة” على غرار ما يقع في الإعلامية (la bogue). أمّا بالنسبة إلى النّماذج البنائيّة، فيتمتّع الخطأ بمكانة أكثر إيجابيّة.  وقد استحال علامة مهمّة لعوائق تكبّل تفكير المتعلّم. فهو الكاشف للتّمشّيات الذّهنيّة للمتعلّمين والمساعد على تعقّلها.  ويتكثّف الاهتمام ـ داخل النّماذج البنائيةـ بتأويل الخطإ وكشف منطقه للاستفادة منه في تحسين التّعلّم. ويوضّح الجدول التّالي مكانة الخطإ داخل النّماذج المذكورة أعلاه:

	الخطيئة (la faute)	هفوة في البرمجة (la bogue)	العائق (l’obstacle)
مكانة الخطإ	نبذ الخطإ.		تثمين الخطإ.
مصدر الخطإ	مسؤولية التّلميذ الّذي كان بإمكانه تحاشيه.	خلل متكرّر في التّخطيط.	صعوبة موضوعيّة لتملّك محتوى مدرّس.
كيفيّة المعالجة	تقييم بعدي لمجازاته.	تقييم قبلي للتّوقّي منه.	عمل داخل السّياق الّذي حدث فيه لمعالجته.
النّموذج البيداغوجيّ المرجعيّ	النّموذج التّمريري	النّموذج السّلوكي	النّموذج البنائي

(Astolfi، 1997، المصدر السّابق، ص 23)

Iـ3ـ حدّ الخطأ

يميّز كلّ من  Briand.JوChevalier M.C (1995) ⁽⁴⁾ بين الإخفاق (l’échec) والخطإ: نعتبر أنّ التّلميذ في حالة إخفاق عندما يحصل على نتيجة مغايرة لما ينتظره ولا تكون لديه البدائل الّتي تمكّنه من إعادة المحاولة بنجاح. ونقرّ بوجود خطإ عندما يكون لدى المتعلّم وسائل تمكّنه من تعديل عمله انطلاقا من نتائج المحاولة السّابقة. ذلك أنّ الوعي بوجود خطإ ما يقتضي امتلاك فكرة قبليّة أو تصوّرا معيّنا أو فرضيّة وفي غياب ذلك يصيب الإخفاق المتعلّم ويستبدّ به.

ويعتقد  (1986) Charnay.R⁽⁵⁾ وجود رأي سائد مفاده أنّ مادة الرّياضيات تُمكّن دائما من القطع بين الصّواب والخطإ. ويرى أنّه إذا ما تأمّلنا تاريخ الرّياضيات فإنّنا لا نجد أساسا متينا لذلك الرّأي، خاصة إذا ما استحضرنا أزمة الأسس الّتي شغلت الرّياضيين كثيرا والإشكاليات الّتي أثارتها الهندسات اللاإقليدية… فالاستدلال الرّياضي لا يقود بسهولة للحسم بين الصّواب والخطإ!  ويضيف  (1986) R. Charnay ⁽⁶⁾ أنّ الأمر نفسه يُوجد في التّعليم: فالحقيقة لا تكون نهائيّة: فالتّعلّمات الرّاهنة والّتي تُقدم على أساس أنّها حقيقة يمكن أن تُوضع موضع الشكّ مستقبلا (بناء على مفهوم العائق مثلا). ورغم هذه التّحفظات، يُمكن أن نعتبرـ في هذه الدّراسة ـ أنّ إجابة المتعلّم خاطئة عندما تكون مخالفة تماما للمعرفة الرّياضية المعترف بها رسميّا من طرف علماء الرّياضيات في الوقت الرّاهن

IIـ التّأصيل النّظري للخطإ

IIـ1 ـ الخطأ من وجهة نظر نفسيّة ـ نشوئيّة وإبستمولوجيّة

سنحاول ـ الآن ـ الغوص في عمق السّيرورات المؤديّة إلى الخطإ بالاستناد إلى أعمال كلّ من G. Bachelard وJ. Piaget ذلـك أنّ مفهومــيْ “العائــق” (l’obstacle) و”الشّــام” (le schème) يمكن أن ينيرا لنا السّبيل.

IIـ1 ـ1ـ الخطأ من وجهة نظر Bachelard

يطرح Bachelard قضية اكتساب المعرفة العلميّة وتطورّها من خلال مفهوم العائق الإبستمولوجي، لأنّه يفضي إلى قطيعة دونها لا يمكن الحديث عن التّقدّم. ويعتقد هذا المؤلف أنّنا لا نتعلّم إلاّ على أنقاض معارف سابقة تتعارض مع المعارف العلميّة. ذلك أن الفرد ـ حسب Bachelard-يأتي إلى العلم دائما كهلا: عمره عمر أفكاره المسبقة وعاداته. فلا بدّ إذن من عمليّة تحليل نفسي للعقل.

وبيّن Bachelard (1977) ⁽⁷⁾ بوضوح كيف أن مفهوم العائق الإبستمولوجي يمكن أن يجد له تطبيقات ثريّة في ميدان التّربية لذلك يقول” يمكن أن ندْرس مفهوم العائق الإبستمولوجي من خلال التّطور التّاريخي للفكر البشري كما يمكن أن ندرسه داخل الممارسة التّربويّة…”.

ولكي نفهم مصادر الأخطاء وتنوّعها برويّة علينا أوّلا إبراز خصائص العوائق الإبستمولوجيّة كما وصفها: M. Fabre في مؤلفه “Bachelard éducateur ” (1995) ⁽⁸⁾ حيث بلغ المؤلف بمفهوم العائق درجة من لطف البيان ما جعله أداة ناجعة لسبر أغوار الأخطاء:

*العائق داخليّ: العائق البشلاردي ليس خارجيّا. بل يسكن الفكر نفسه. يسكن الكلمات والتجربة الأولى واللاّوعي. ومن هذا المنظور، يصبح الخطأ مكوّنًا من مكوّنات فعل المعرفة نفسه. لهذا نفقد كلّ أمل في تجنّب العوائق لأنّها ملازمة لعمليّة التّفكير.

*سهولة العائق: يفيد العائق ـ هناـ ميل الفكر الإنساني إلى السّهولة عند مواجهة المسائل المعرفيّة. إذ يلتجأ دائما إلــى التقــــاط الانتظامات والقيام بالمماثلات والتّعميمات المفرطة. فهو يعكس المنحدر الطبيعي للتّفكير الإنساني.

*إيجابيّة العائق: وفق ما تقدّم، يتجلّى العائق رأيا (بالمعنى الأفلاطوني) لم يُساءل بعدُ. وبٱختصار، لا يمثّل العائق معرفة رثيثة. بل هو شكل من أشكال المعرفة.

*غموض العائق: من زاوية أخرى، العائق نسبيّ: بمعنى نمط من التّفكير له صلوحيّة محدّدة. فمثلا تصوّرات الفرد تشتغل ـ حسب السّياق ـ تارة أداة ناجعة وطورا عائقا.

*تمظهرات العائق: يتمثّل المظهر الأوّل للعوائق في انغراسها المتنامي في الذّهنيّة الفرديّة. فهي تعكس المستوى العميق من تصوّرات المتعلّمين. ويبرز مظهرها الثّاني في ارتباطاتها على أكثر من مستوى. فهي لا تقتصر على الميدان العقلي فحسب، بل تمتّد إلى الجوانب الانفعالية والوجدانية والعاطفية والسّحرية… إذْ تملك شحنة رمزية قويّة. لذلك فكلّ تغيير يشمل العوائق ينتج عنه تعديلات تمسّ جوهر هُويّة الفرد.

ويُفرّق M. Fabre (1999) ⁽⁹⁾ بين العائق المُولِّد لأخطاء عادية تَسِم عادة عمليّة نشوء المعارف، والتعّطل النّفسي الناتج عن بعض الخصائص المميّزة للفرد، وأيضا بين العائق والصّعوبة الناجمة عن تعقّـد المسائـل. لذلك ما يدلّ على العائق حقا هو ذلك الخطأ العاديّ والعام والمتكرّر والمقاوم والّذي يختفي ليعود من جديد.

في المحصّلة، لا يدلّ العائق على خلل في الاشتغال لدى المتعلّم ولا هو بالصّعوبة الّتي يصطدم بها فكره. بل هو شاهد على البطء الّذي يميّز كلّ فكر بصدد البناء. وتبعا لذلك ينكشف الخطأ أثرا لنشاط ذهنيّ أصيل وظاهرة مرافقة لكلّ عمليّة تهيئة ذهنيّة حقيقيّة.

IIـ1 ـ2ـ الخطأ من وجهة نظر Piaget

تؤكد مقاربة Piaget على ضرورة احترام مراحل النّمو لدى المتعلّم وعدم القفز عليها.

ففي طرح Piaget، يقابل مفهوم الشّام مفهوم العائق لدى Bachelard. ويعتبرPiaget الشّامات وسائل معرفيّة يمتلكها الفرد لفهم الواقع الخارجي وتأويله. وهي تتموقع في مستويات مختلفة: من الشّامات الحسيّة ـ الحركيّة الّتي تميّز الطّفولة الأولى (شامات المصّ أو المسك) إلى الشّامات الإجرائيّة الأكثر تعقيدا والخاصّة بالتّفكير الشّكلي (شامات التّناسب) مرورًا بطائفة متنوّعة من شامات الفعل.

ويوضّح J.P Astolfi (1997) ⁽¹⁰⁾ أنّ الشّام يتمثّل فيما هو ممكن، في ما يوجد بالقـوّة. لذلك فإنّه لا يعني الفعل نفسه ولكن بنية عامة مشتركة لمجموعة من الأفعال. فالشّـام يمثّـل كلّيـة أي مجموعة متناسقة من العناصر تشترك مع بعضها وتُؤمّن المعنى الشّامل للفعل. وهو يتميّز عن الآلية أو الإشراط.

أمّا M. Fabre (1999) ⁽¹¹⁾ فيرى أنّ الشّام يمثّل بعدا رئيسيا للتّمثل: فهو أداة يبنيها الفرد لفهم العالم والتأثير فيه. هذه الأداة تحافظ على شكلها من خلال التّكرار وتتدعّم من خلال الفعل وتُعمّم وتتميّز حسب الأوساط وأخيرا تتناسق مع شامات أخرى داخل بنيات أوسع. فمن شامات الفعل (مثل شام المـصّ أو شام الشّيء القار…) إلى الشّامات الإجرائيّة (مثل شام الجمع، أو شام التّعريف…) يمكن أن يُقرأ النّمو تنظيما نشطا للتّجربة يتهيكل بإدماج الماضي وتعاد هيكلته من جديد في ضوء ما يتطلّبه الحاضر من تكيّفات جديدة.

ويُلخّص فكر Piaget بشكل عام حول هذا الموضوع بأنّ التّوازن النّاجح هو الّذي:

– يسدّ الفجوات الّتي يعكسها التّوازن السّابق،

– يُدمج البنى الضامنة للتّوازن السّابق في بنية جديدة،

– يخلق انفتاحا على ممكنات جديدة.

وتعكس أخطاء المتعلّمين ـ من وجهة النّظر هذه ـ الكيفيّة المخصوصة الّتي من خلالها تنتظم الشّامات عبر مختلف مراحل نموّ الفرد. وأنّ الكثير من إجابات المتعلّمين الّتي تبدو غريبة بالنسبة إلى من يعرف الإجابة الصحيحة، تدلّ ـ في الواقع ـ على استعمال المتعلّمين لاستراتيجيات معرفيّة “مؤقتة”. وبعبارة أدق، يعتبر الخطأ، اعتمادا على مقاربة Piaget، دليلا على وجود انعدام توازن لدى الفرد: فهو يبرز الفشل المؤقت لاستعمال استراتيجية تكيّفيّة معّينة. فهو شاهد على إخفاق شام معّين!

بناء على ما تقدّم، نصبح أكثر إيقانا بأهميّة الخطأ. بل يصبح مكوّنا من مكوّنات سيرورة التّعليم ـ التّعلّم.

IIـ2 ـ الأخطاء… التّصوّرات… العوائق… وتعلّميّة الرّياضيات

لقد أبرزت الدّراسات في تعلميّة الرّياضيات وجود أنواع من الأخطاء المخصوصة ذات صلة بالمفاهيم المدرّسة. وتمتاز هذه النوعية من الأخطاء بكونها متكرّرة وعامّة وشديدة الصّلابة ومقاومة لكلّ تغيير. الأمر الّذي قاد العديد من المختصّين إلى اعتبارها مؤشرا دالاّ على وجود معرفة بحاجة إلى تعديل أو على تصوّرات ـ عوائق تحول دون المتعلّم وتملّك المفاهيم الرّياضيّة.

ويعرّفJean Migne ⁽¹²⁾ التّصوّر “بأنّه نموذج شخصيّ لتنظيم المعارف بالنسبة إلى مسألة معيّنة… وأنّ الاختلاف بين المفهوم العلميّ والتّصوّر ليس اختلافا في الدّرجة بل أنّ كلّ واحد منهما يكوّن نموذجا مختلفا للمعرفة …فالمفهوم يمكن اعتباره عقدة في شبكة من العلاقات المحدّدة بشكل عملياتي بينما التّصوّر هو نموذج معرفي يغلب عليه الطّابـع الرّمـزي l’aspect figuratif)) … ” وقد بيّنت عديد الدّراسات الطّابع المركّب الّذي يميّز التّصوّرات. لذلك يحصر Astolfi (1997) ⁽¹³⁾ مصادرها المتنوّعة وأسبابها في النّواحي التّالية:

1) يمكن اعتبار عدم اكتمال النّمو الذّهني للفرد- إذا ما استندنا مثلا إلى نظرية Piaget ـ مصدرا من مصادر التّصوّرات الخاطئة. وتفسّر التّصوّرات الخاطئة في هذه الحالة:

*بهيمنة الوظائف الرّمزيّة على الوظائف العملياتيّة،

*أو بالاحتفاظ ببعض مظاهر الاشتغال الذهنـي المميّز للطّفولة: مثل الغائية والإحيائيـة والاصطناعية….

*أو أنّ الطّفل مــازال لم يبـن بــعدُ الشّامــات والـبنيات الّتي تــمكّن من المعكوسّية العملياتيّة (la réversibilité opératoire).

2) وإذا اعتمدنا نظرية Bachelard إطارا مرجعيّا، فإنّ المعارف العامّة والتّجريباتيّة ومركب الانطباعات الأوّليّة تُعتبر مصادر للتصّورات -العوائق حيث يصبح من الضّروري القطع معها.

3) ويمكن أن يكون مصـدر هذه التصّورات مـا هو نفسي – اجتماعي كمــا أُبــرز ذلـــك S. Moscovici   حيث اعتبر هذا الأخير التّصوّر الاجتماعي أسلوبا معرفيّا مميّزا له وظائف تتّصل بسلوكات الأفراد وتواصلها. وأنّ عمليّة إدماج المعارف العلميّة في الإطار الاجتماعي تقتضي إيجاد قطيعة.

4) وأخيرا يمكن ربط بعض التّصوّرات بتاريخ الفرد. فإذا اعتمدنا التّحليل النّفسي إطارا، فإنّ بعض تصوّرات المتعلّمين تعكس سيرورات النّقل مثلا في ارتباطها بالطّاقة اللّبيديّة.

لئن اختلفت المواقف في تحديد مصادر التّصوّرات وأسبابها فإنّ جلّ الدّراسات تشير بوضوح إلى أنّ تّصوّرات المتعلّمين تشكّل نظاما مفاهيميّا ونظاما تفسيريّا يُوظّـفهما المتعلّم لتفسير حالة أو وضعية تقدّم له. وتجدر الإشارة إلى مرونة تلك التّصوّرات وقدرتها على التّكيّف مع الوضعيـات والتّعايش مع بعضها من خلال انتظامها داخل سجلاّت مَسِيكَة. وهذا ما يفسّر صلابتها وتعنّتها وصُمودها إذا تعلّق الأمر بزعزعة نظامها. لذلك يقول  Astolfi ⁽¹⁴⁾ “تُحدّد قيمة التّعليم الحقيقيّ عن طريق التّغييرات الّتي يحدثها في تصوّرات المتعلّم من ناحية وقيمة المعرفة العلميّة الّتي يقدّمها المدرّس من ناحية أخرى قصد إعانة المتعلّمين على بناء المفاهيم العلميّة.”

إذن، يصبح التّعلّم من هذا المنظور هو القدرة على تغيير نظام التّصوّرات استنادا إلى أخطاء المتعلّمين المخصوصة. 

IIIـ الجوانب التّطبيقيّة المتّصلّة باستثمار الخطأ وفق المرجع النّظري أعلاه

يلخّص PH. Meirieu (1994) ⁽¹⁵⁾ بشكل بليغ المكانة الّتي أصبح يتمتّع بها الخطأ حيـث يقـول: “… كان لا بدّ من وجود أماكن حيث يمكن أن نخطئ دون أخطار أو مجازفة وحيث يمكننا تحليل أخطائنا حتى لا تتكرّر… وأعتقد أنّنا قد نسينا أنّ من أجل ذلك بالأساس بعثت المدرسة. وهو المكان الّذي يكون فيه الخطأ ممكنا، لأنّ المدرسة مكان يكون فيه التّحسّس والتّردّد ضروريين ويكون فيه التّعلّم تدريجيّا.”

وتبعا لذلك بوّأ التّربويون المعاصرون الخطأ منزلة هامّة للأسباب التّاليّة:

* أنّ الخطأ هو رسالة موجّهة إلى المدرّس وما على هذا الأخير إلاّ أن يفكّ رموزها حتّى يحصل على معلومات حول التّمشّي الّذي اتّبعه المتعلّم.

* أنّ الخطأ لا يعتبر هاما في حدّ ذاته. فالأهمّ هو التّمشّي الّذي قاد إلى حصوله وأنّ معرفة ذلك التمشّي أمر ضروريّ إذا ما رُمنا إدخال التّعديلات اللاّزمة لمعالجة أسباب الأخطاء.

* أنّ الخطأ لا ينتج بالضرورة ـ كما يتبادر للذّهن عن عدم الانتباه ـ بل أنّه يخضع في العديد من الحالات إلى منطق معيّن. فقد يعكس تأثير تصوّرات سابقة. تكون هي العلّة في حدوث الخطأ، وتقف عائقا أمام اكتساب معارف جديدة.

وصفوة القول، يمكننا اليوم الإقرار بضرورة حيازة المدرّس على كفايات تمكّنه من بناء أجهزة علاجيّة ناجعة يستثمر من خلالها أخطاء المتعلّمين ببراعة بما يجوّد تعلّماتهم.

III ـ1ـ العلاج إستراتيجيّة بيداغوجيّة

يعرّف Raynal.F وRieunier.A (1998) ⁽¹⁶⁾ الاستراتيجيّة البيداغوجيّة بأنّها: “تنظيم لجملة من التّقنيات والوسائل لغاية تحقيق هدف بيداغوجي”

أمّا الإستراتيجيّة العلاجيّة الّتي نقصدها في دراستنا هذه: فهي لا تعدو أن تكون سوى تطبيقا لتمشيات التّقييم التّكويني: ” تقييم ـ تشخيص-علاج-تقييم” ويمكن تفصيل مراحلها على النّحو التّالي:

1) تقييم مكتسبات المتعلّمين بعد إنهاء ما هو مقررّ بالمنهاج الرّسمي،

2) استغلال نتائج التّقييم لـ:

* تعرّف الأخطاء المتكررّة والمشتركة ورصد مواطن الخلل،

* تقديم فرضيات متنوّعة في غير ٱحتراز حول السّيرورات المستعملة من طرف المتعلّمين والّتي أدت بهم إلى تلك الأخطاء وكذلك حول مصدر تلك السّيرورات،

* التّثبت من تلك الفرضيات قبل ٱعتمادها بشكل نهائيّ.

وتمثّل الخطوات السّابقة مرحلة التّشخيص.

3) في ضوء الفرضيات الّتي اعتمدت حول مصادر الأخطاء، تُحدّد نوعيّة العلاج والجهاز البيداغوجي.

4) إجراء تقييم بعدي للتّثبت من نجاعة العلاج الّذي استخدمنا.

ويمكن إبراز ّ تلك المراحل من خلال الرّسم التّالي:

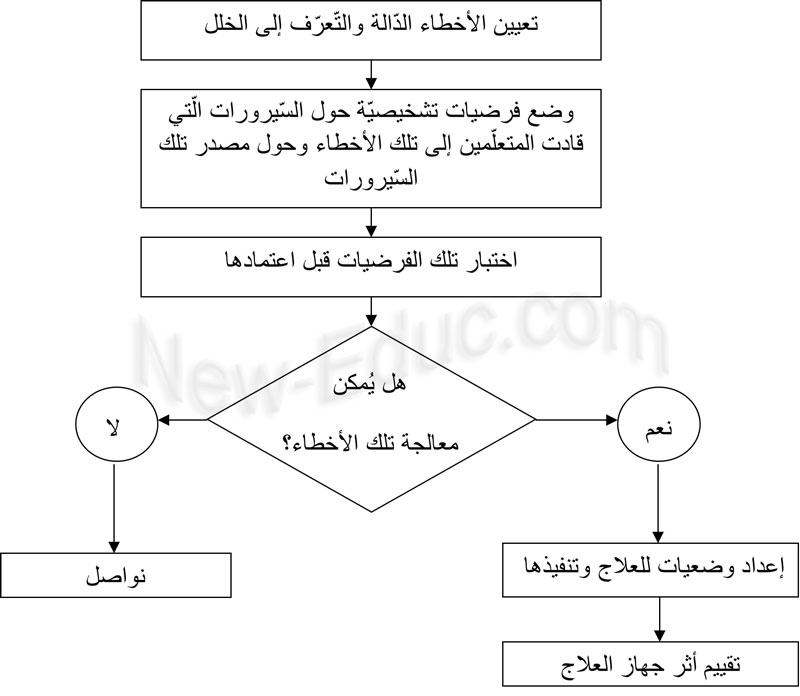
ويشيرR.Charnay (1992) ⁽¹⁷⁾ إلى أنّ عملية تحليل الأخطاء هي دالة تصورّنا للتّعلّم أي إجابتنا عن السّؤال: كيف يتعلّم تلاميذنا؟ بينما جهاز العلاج هو دالة تصورّنا للتّعليم أي إجابتنا عن السّؤال: ما الّذي يجب أن يميّز الأنشطة الّتي سوف تُقترح على التّلاميذ لتيسير عمليات التّعلّم وتعديلها؟ وتُعدّ عمليّة تحليل الأخطاء والوقوف على مصادرها من أصعب المهام المنوطة بعهدة المدرّس. وأنّ جلّ المدرّسين يجدون صعوبات متنوّعة في هذا المجال.

III ـ2ـ مصادر الأخطاء في الرّياضيات و طرق علاجها

يعتمد Charnay.R(1992) ⁽¹⁸⁾ المنظومة التّعلّمية التّعليميّة بأقطابها الثلاثة (مدرّس، متعلّم، معرفة) مرجعا لتحليل اختيار المدرّس للمهام التّعليميّة ولتحليل أخطاء المتعلّمين وتأويلها ومعالجتها.

فمثلا يمكن تحليل مهمّة مقترحة من لدن المدرّس:

– من خلال بعض الخصائص الفرديّة للمدرّس (مثل تصوّراته المتّصلة بالتّعلّم والتّعليم) وفي هذه الحالة نركز على قطب “المدرّس”،

– أو من خلال توزيع المدرّس للمحتوى الرّياضي والأهداف النّوعيّة الّتي يعطيها الأولويّة وفي هذه الحالة نركّز على العلاقة ” مدرّس-معرفة”،

– وأخيرا من خلال تصوّر المدرّس لحالة المعارف الراهنة لدى المتعلّمين.

ويكون هذا النوع من التّحليل مهمّا عند إعداد جهاز العلاج.

وبالمثل يمكن تحليل تصوّر المتعلّم للمهمّة المقترحة عليه ومعالجته لها والأجوبة الّتي يقدّمها وكذا الأخطاء الّتي يرتكبها:

– من خلال خصائصه الفرديّة، ونركّز حينئذ على قطب “المتعلّم”،

– أومن خلال معارفه الراهنة وتصوّراته الّتي استخدمها لمقاربة المهمّة. ونركز حينئذ على العلاقة ” متعلّم-معرفة”،

– وأخيرا من خلال تأويله للوضعيّة التّعليميّة والمهمّة المقترحة عليه ويكون هذا التأويل عادة متأثّرا بالعقد التّعلّمي التّعليمي السائد. ونركّز في هذه الحالة على العلاقة “مدرّس-متعلّم“. 

ويكون هذا النّوع من التّحليل مفيدا عند تشخيص أخطاء المتعلّمين وتأويلها.

ونعرض فيما يلي تجسيدا عمليا لهذه الإستراتيجية التّحليليّة بالتّركيز حصريّا على قطب المتعلّم وعلى علاقته بالمدرّس والمعرفة:

تحليل مرتبط بخصائص المتعلّم [القطب “متعلّم”]

ويمكن أن نورد تباعا:

* الأخطاء المتولّدة عن عدم اكتمال النّموّ المعرفيّ والذّهنيّ للمتعلّم،

* الأخطاء الّتي يمكن تفسيرها بمحدوديّة قدرة المتعلّم في مجال معالجة المعلومة،

* وأخيرا الأخطاء الّتي يمكن ربطها ببعض الخصائص الفرديّة المميّزة لمتعلّم ما.

ويلخّص الجدول التّالي الحالات المذكورة أعلاه:

تحليل الأخطاء بالاستناد إلى قطب ” المتعلّم “
مصدر الخطأ	مثال	علاجه
خطأ مصدره انتوجينيكي (Erreurs d’origine ontogénique)	يجيب بعض التّلاميذ من السّنة الثّالثة أساسي على المسألة التّالية باستخدام الجمع: “لعب سامي مع أصدقائه لعبة الكجّات. فربح 6 كجّات. الآن أصبح لديه 17 كجّة في الجملة. كم كان يملك عند بداية اللّعب؟” يتطلّب الحلّ القانوني لهذه المسألة استعمال عمليّة الطرح. أي إجراء حساب علائقي (تعويض تحوّل إيجابي بتحوّل سلبي للحصول على وضعية الانطلاق). ويستوجب هذا الأمر التّمكن من شامات المعكوسيّة الإجرائيّة الّتي تبنى بعد سنّ التّاسعة. (La réversibilité opératoire)	*هنالك من يرى ضرورة احترام المرحلة النّشوئيّة الّتي يمرّ بها المتعلّم وبالتّالي العدول عن تقديم مسائل تتجاوز قدراته المعرفيّة. *والبعض الآخر يرى إمكانية تدريب المتعلّمين على بعـض العمليات الذّهنيّة العامّة (مثل المعكوسيّة) من خلال القيام بأنشطة داخل ورشات للاستدلال المنطقي. (Ateliers de raisonnement logique) . (J.M.Dolle)
أخطاء مصدرها محدوديّة قدرات المتعلّمين في مجال معالجة المعلومة: ونقصد بالتّحديد حالات العبء المعرفيّ. (La surcharge cognitive) ونذكّر بأنّ علماء النفس العرفانيين يميّزون بين نوعين من الذّاكرة: * الذّاكرة طويلة المدى: وتعتبر خزّان المعلومات المتراكمة لدى الفرد عبر السّنين. لكن يصعب في بعض الحالات استدعاء بعض المعلومات منها. * وذاكرة العمل: حيث تتدخّل باستمرار في نشاطات الفرد حتّى تبقى المعلومات الّتي هي بصدد المعالجة جاهزة مؤقتا. وتختصّ هذه الذاكرة بمحدوديّة مزدوجة: من حيث السّعة (عدد محدود من العناصر يُمكن الاحتفاظ بها) ومن حيث الزّمن (لفترة قصيرة جدّا). وتنتج حالة العبء المعرفي عندما تشتغل ذاكرة العمل على أنشطة معرفيّة غير آلية الأمر الّذي يقود إلى تضاؤل القدرة على الخزن نتيجة التّنافس الّذي يحدث بين أنشطة معالجـة المعلومات وأنشطـة التّكرار الذّهني للاحتفاظ بها. وتسهم العوامل التّالية في تفاقم حالات العبء المعرفيّ: *القيام في آن بعدّة أنشطة، *غياب التّمشّيات الآلية الأمر الّذي يتطلّب بناءها من جديد جزئيا أو كلّيا، *تعلّق الفرد بالألقوريتمات مكلفة معرفيّا (مثل القيام بعملية قسمة من خلال عدّة عمليات طرح)، *غياب بعض الأحداث من سجلّ الذّاكرة طويلة المدى (نتيجة عدديّة، رسوم لبعض المسائل …)	أبرز J.F Richard (1982) كيف تتجلّى محدوديّة ذاكرة العمل من خلال نشاط حلّ المشكلات: ذلك أنّ حلّ المشكلات يتطلّب: * في مرحلة أولى فهم نصّ المشكل. فإذا لم تتمّ القراءة بطريقة آلية فإنّها تتسبّب في عملية شحن ذهنيّ مهمّة يمكن أن تنافس نشاط الخزن. الأمر الذي يقود إلى تجاوز قدرة المتعلّم الذاكريّة أو الزّهد في قراءة النصّ وبالتّالي عدم التّعمق في فهمه. ويلجأ المتعلّم حينئذ إلى استعمال بعض القواعد العائدة للعقد التّعليمي أو التّركيز على ما توحي به بعض الكلمات من معاني مثل كلمة “أضاف” تصبح مرادفا لعملية الجمع. *ويفترض حلّ المشكل أيضا القيام بعدّة معالجات مثل: ـ الاحتفاظ في الذاكرة بالنتائج الوسيطة والأهداف الفرعيّة الّتي ينبغي تحقيقها ـ ومراقبة تنفيذ التّمشي المعتمد والألقوريتمات المستخدمة. ويستدعي إنجاز كلّ هذه المهمّات تنشيط ذاكرة العمل ونظرا لمحدودية هذه الأخيرة فإنّ نسيان بعض المعطيات أو بعض الأهداف أو حتّى مخطط الحلّ الأصلي أمر وارد جدّا. ونقترح مثالا توضيحيّا لما تقدّم: 1) قُدّم هذا التّمرين إلى تلاميذ السّنة الثّالثة من التّعليم الأساسي في إطار الحساب الذّهني: *  نصّ التّمرين:  36 + 24 كم تساوي؟ (ذهنيّا). * عديد الإجابات كانت خاطئة. 2) ويمكن تفسير أخطاء المتعلّمين على النّحو التّالي: يُفسّر الخطأ بحالة العبء المعرفي الّتي تنتاب متعلّم السّنة الثّالثة عند حسابه لهذه العملية ذهنيّا. ذلك أنّ على المُتعلّم القيام بالإجراءات التّالية للوصول إلى الحلّ: ·       خزن العددين 24 و36 وكذلك نوع العمليّة في ذاكرة العمل، ·       يعتمد على ذاكرة العمل للقيام بتفكيك العددين وذلك من خلال استدعاء تمشٍّ مخزون بالذّاكرة طويلة المدى: 36=30 +6 على أساس أنّ العدد الثّاني ينتهي ب رقم4. ثمّ يفكك العدد الثاني:24=4+ 20 وتخزين التّفكيكين في ذاكرة العمل ثمّ استرجاع من الذّاكرة طويلة المدى نتيجة: 4 + 6 = 10 و30 + 20 = 50. وإذا تعذّر ذلك، عليه أن يعيد بناء هذا التّمشي وهو ما يفترض معالجة أخرى إضافية من ذاكرة العمل… نلاحظ هنا أنّ العبء المعرفيّ يحدث عندما يتعذّر استرجاع بعض النتائج العدديّة من الذّاكرة طويلة المدى أو عندما تكون بعض التّمشيات غير آلية.	1)  تُبرز بعض الدّراسات بأنّ تحسين قدرات ذاكرة العمل يُعتبَر أمرا صعبا. ولكن بالمقابل يمكن مساعدة المتعلّمين على التّخفيف من حالات العبء المعرفي ببناء عدّة إواليات لدى المتعلّم: مثل التّقنيات الإجرائية، والتّعرّف إلى الأشكال الهندسيّة المعروفة، وتنظيم العمل، والتّدرّب على القراءة السّريعة…. ونحقّق هذا الغرض من خلال تمارين متدرّجة ومتنوّعة ومتكرّرة. 2) وبشكل عام، يمكن أن نلخّص الصّعوبات المتعلّقة بحلّ المشكلات وعلاجها على النّحو التّالي: ü    صعوبات على مستوى بناء تصوّر ملائم للمشكل: عندما يكون: *سبب إشباع ذاكرة العمل يتمثّل في عدم التّمكّن من آليات القراءة ¬  قراءة نصّ المسألة على التّلميذ مع برمجة أنشطة موازية لتحسين قدرته على القراءة. *السّبب يتمثّل في عدم قدرة المتعلّم على اختيار المؤشّرات الملائمة للمشكل ¬ تدريب المتعلّم على تشخيص الوضعيّة من خلال رسمها ذلك أن هذا التّصـوّر المجـازي للوضعيّة يخفّف من حدّة الشّحن الذّهني…. *السّبب يتمثّل في بعض قواعد العقد التّعليمي (مثل كلّ مسألة لها حلّ، وللتّوصل إلى ذلك يجب توظيف المفهوم موضوع الدّرس الجديد) ¬ يتمثّل الحلّ في كسر هذه القواعد الضمنيّة. ü    صعوبات على مستوى بناء استراتيجيّة لحلّ المشكل: عندما يتمثّل: *السّبب في وجود نقص في التّجارب الاجتماعية والمدرسيّة المخزّنة بالذاكرة طويلة المدى ¬العمل على إثراء رصيد المتعلّم من التّمشيات والمشاكل المرجعيّة. *السّبب في صعوبة استرجاع بعض التّمشيـات والمسائل المرجعيّة من الذّاكرة طويلة المدى ¬اقتراح مشاكل تستدعي استخدام تمشيات متنوّعة وإعطاء الفرصة للمتعلّم لكي يعبّر عن التّمشيات الّتي استعملها والصّعوبات الّتي تعرّض إليها… ü    صعوبات على مستوى تنفيذ الاستراتيجيّة المعتمدة: عندما يكون: *السّبب في سوء التّصرّف في استخدام الاستراتيجيّة المعتمدة ¬ مساعدة المتعلّم على تنظيم عمله أو القيام بأنشطة على مستوى مجموعات صغيرة. *السّبب في عدم التّمكّن من بعض التّقنيات الإجرائية ¬ العمل على بنـاء بعض الإواليات.
أخطاء عائدة للخصائص الفرديّة للمتعلّم:	* تصوّر المتعلّم لمادة الرياضيات يمكن أن يكون سببا في رفض هذه المادة ومصدرا لأخطاء متنوّعة. وقد أبرزت أعمال J. Nimier (1973) أنّ تعلّم الرّياضيات يُصحبُ في كثير من الأحياء بمعيش وجدانيّ قويّ وأنّ اللاّوعي قد يستخدم الرّياضيات ليجعل منها موضوعا خطيرا قد يؤدّي إلى الإخلال بالنّموّ السّويّ للشخصيّة. ويدفع ببعض المتعلّمين إلى تكوين نظام دفاعي يتمثّل في الرغبة في الإخفاق في الرّياضيات. * يمكن أن يكـون مصـدرا لعـدّة أخـطـاء تصوّر المتعلّم لذاته كرياضي حيـث أبـرزR. Noirfalise (1990) بأنّ التّلاميذ “الممتازين” عندما يخطئون يطوّرون برنامجا للمعالجة يمكّنهم من النّجاح في المرّات القادمة. بينما التلاميذ “الضّعفاء” سرعان ما يهجرون تلك البرامج العلاجيّة بما يدعم لديهم تصوّرا سلبيا لذواتهم في مادّة الرّياضيات.	* إرساء حوار مع المتعلّمين ذوي الصّعوبات من أجل إقناعهم بإمكانية الحصول على نتائج أفضل. * تثمين الأعمال الصّائبة الّتي يقومون بها. * اقتـراح وضعيـات ـ مشكـل مفتـوحـة على المتعلّمين تمكّن الجميع من محاولة تجريب عدّة تمشّيات بما يساعد على الرّفع من دافعيتهم وبالتّالي التّخلّص من بعض التّصوّرات المكبّلة لنشاطهم.

تحليل مرتبط بتصوّرات المتعلّمين للمعرفة الرّياضيّة [العلاقة: متعلّم¬ معرفة]

تتحوّل تصوّرات المتعلّمين ذات الصّلة ببعض المفاهيم الرّياضية إلى عوائق خلال تمشي اكتساب المعارف ويمكن ضبط مصادرها على النّحو التّالي:

– تصوّرات ـ عوائق مصدرها إبستمولوجي،

– تصورات ـ عوائق مصدرها تعلّمي،

تصوّرات ـ عوائق مصدرها نشوئي (انظر التّحليل السّابق).

ويلخّص الجدول التّالي الأخطاء الّتي يكون مصدرها تصوّرات ـ عوائق وكيفيّة علاجها:

تحليل الأخطاء بالاستناد إلى العلاقة: [متعلّم ¬ معرفة]
مصدر الخطإ	مثال	علاجه
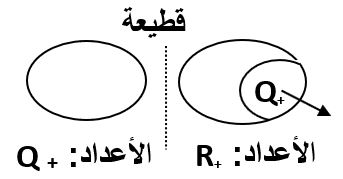
تصوّرات ذات علاقة بعوائق مصدرها إبستمولوجي:   يتعلّق الأمر هنا بتصوّرات ـ عوائق برزت في تاريخ تكوّن المفهوم الرّياضي. وقد أدّى رفضها والتّخلّى عنها إلى بناء المفهوم. ووفقا للنظريّة التّلخيصيّة، فإنّ المتعلّم يعيد نفس الأخطاء ويتعرّض لنفس الصّعوبات الّتي تعرّضت لها الإنسانيّة عند بنائها لمفهوم رياضي محدّد.	– شكّل التصور الذي كان سائدا لدى الرّياضيين اليونانيين والّذي يفيد بأنّ الكميات كلّها قابلـة للمقارنة وبالتّالي كسريّة عائقا أمام بناء نظرية الأعداد الحقيقيّة. وتجاوز الرّياضيون اليونانيون   هذا العائق ـ وبالتّالي إحداث قطيعةـ عندما انتقلوا من وضعية يعتبرون فيها “كلّ عدد هو كسر” إلى وضعيّة جديدة “من بين الأعداد بعضها كسريّ”. ويمكن إبراز هذه القطيعة على النّحو التّالي:	يتمثّل الرّهان التّعليمي في إقناع المتعلّم بمحدوديّة تصوّره وإبراز التّناقض الحاصل بين ما يتصوّره وبين الحقيقة الرّياضيّة. وننجح في ذلك باستخدام الطرق التّاليّة:* إجـراء مقـابلــة للتّـوضيـح مـع المتـعلّم (entretien d’explicitation) يعبّر فيها عن التّمشّيات الّتي استخدمها وهذا الأمر يمكّنه من الوعي بتناقضاته. * تنظيم صراعات معرفيّة اجتماعية بين المتعلّمين يكون محتواها مختلف التّصوّرات السائدة وتجدر الإشارة إلى أنّ هذا النوع من التّقنية لا ينجح إلاّ إذا تحوّل الصراع من المستوى الاجتماعي إلى المستوى الدّاخلي لكلّ متعلّم لذلك وجب الحرص على تنظيم المجموعات والتّصرّف في الفصل بشكل يحقّق هذه الغاية. * اقتراح وضعيات ـ مشكل تسمح للمتعلّم باستخدام تصوّراته والوقوف على محدوديتها من خلال الوضعيّة نفسها دون أيّ تدخّل من المعلّم.
تصوّرات عوائق مصدرها تعلّمي: ترتبـط عديـد الأخطاء المرتكبة من طرف المتعلّمين بتصوّرات ـ عـوائق يكون مصدرها الأوّل جهاز التّعليم: سواء على مستوى تقسيم المحتويات وطرق تقديرها أو اختيار الوضعيات التّعليمية.	يبدأ المتعلّمون بالمدرسة الأساسيّة بدراسة الأعداد الطّبيعيّة. ويتعلّمون بمناسبة ذلك عدّة قواعد. لكن عند الانتقال لدراسة الأعداد العشريّة مثلا، ينزع العديد منهم إلى سحب تصوّراتهم ذات الصّلة بالأعداد الطّبيعية على الأعداد العشرية. وتتدعّم تلك التّصورات الخاطئة عندما تُقدم لهم الأعداد العشريّة كامتداد للأعداد الطّبيعية من خلال مسائل تتّصل أساسا بأنظمة القيس. فنجد مثلا أخطاء أساسها اعتبار المتعلّم أنّ العدد العشريّ يتكوّن من عددين طبيعيين بينهما فاصلة: * 2,4 x 3,2 = 6,8 * 9,16 = 3,4 x 3,4 * 7,4 < 7,16 *الموالي للعدد 3,24هو 3,25 * الضرب يزيد دائما في الكميّة * المقسوم دائما أكبر من القاسم * العدد الأكبر هو الّذي يحتوي على عدد أكبر من الأرقام….

تحليل في إطار العقد التّعلّمي-التّعليمي [العلاقة: مدرّس¬ متعلّم]

يعرّف G. Brousseau ⁽¹⁹⁾ العقد التّعلّمي-التّعليمي على أنّه “مجموع العلاقات الّتي تحدّد بصفة صريحة في بعض الحالات وضمنيّة في أغلبها ما هو مطلوب من المعلّم والمتعلّم أن يقوما به خلال حصّة تعلّميّة-تعليميّة معيّنة”. لذا يمكن وصف العقد على أنّه مجموعة من القواعد (أغلبها ضمني) والّتي تحكم اشتغال الفصل والعلاقات مدرّس-متعلّم. وتُطرح في إطار هذا العقد أسئلة من طرف المتعلّم مثل: ما المطلوب بالضبط؟ ما هو منتظر؟ ما الممنوع وما المسموح به؟

ويُكوّن المتعلّم إجابات عن هذه الأسئلة من خلال رصده لتتابع الأنشطة المقترحة عليه تتّصل ببعض المهام المحدّدة. ويمكن حوصلة الأخطاء العائدة للعقد من خلال الجدول التّالي:

تحليل الأخطاء بالاستناد إلى العقد التّعلّمي-التّعليمي (العلاقة: مدرّس – متعلّم)
مصدر الخطأ	مثال	علاجه
أخطاء مصدرها بعض القواعد كوّنها المتعلّم من خلال العقد والّتي سوف تشتغل عوائق أمام تمثّل المهمّات المطلوبة.	نورد في هذا السّياق عدّة أمثلة حول حلّ المسائل: -البحث عن حلّ واحد للمشكل عندما لا يطلب أكثر من حلّ بشكل صريح. – كلمة “خسر”، تعني القيام بعملية طرح. – لكلّ مشكل حلّ. – لحلّ المشكل، يـجـب استعمال المعلومات الجـديــدة الّتـي تمّ تدريسها. – للوصول إلى حلّ، يجب استعمال كلّ المعطيات الكميّة المقدّمة في المشكل….	لمساعدة المتعلّمين على القطع مع هذه القواعد الخاطئة، يجب البحث عن وضعيات تبرز محدوديتها: لذا يمكن في هذا الإطار استعمال مسائل مفتوحة أو اقتراح مسائل دون أسئلة أو مسائل تنقصها بعض المعطيات.
أخطاء مصدرها عدم تملّك المتعلّمين لبعض القواعد المخصوصة ذات الصّلة بنشاط معيّن. وفي هذه الحالة يخطئ المتعلّم لأنّه لا يعرف بالضبط ما يطلبه المدرّس.	ويمكن ذكر بعض الحالات في هذا السّياق: -إرفاق الإجابة بتفسير أو بتعليل، -درجة الدقّة المطلوبة في البناءات الهندسيّة…. كلّ هذه الحالات تقود المتعلّم إلى الخطأ عندما لا يعرف ما يطلبه المدرّس بالضبط.	يمكن أن تساعد تقنية التّقييم التّكوّني (l’évaluation formatrice) المتعلّمين على تملّك هذه القواعد المخصوصة وذلك من خلال إبراز معـاييـر النجــاح المطلوبـة. (Les critères de réussite).

IV– خاتمة

يتبيّن لنا من خلال التّحاليل السّابقة أنّ ديداكتيك الرّياضيات قد طوّر خطابا متميّزا حول الأخطاء. لكن إذا كان من المهمّ التّعرّف إلى تلك الأخطاء فإن الأهمّ يتمثّل في فكّ رموزها ومساعدة المتعلّمين على تجاوزها. لذلك تقول Stella Baruk ⁽²⁰⁾ (1993) “تمثّل الأخطاء أحسن وسيلة للنظر في ما وقع تمريره من خلال التّعليم. فأخطاء المتعلّمين هي ـ في الواقع ـ أسئلة مطروحة علينا…”  فالأخذ بأخطاء المتعلّمين أثناء التّمشيات التّعليميّة أضحى بمرتبة القاعدة التّعليميّة. وما خرج عن ذلك عُدّ فسادا بيداغوجيّا واضطرابا، لأنّ المتعلّم الضَّعُوف خاصة لا يقوى على تجاوز ضعفه إلاّ إذا استفاد من أخطائه. ولا يمكن بأيّ حال بلوغ تلك الغاية إلاّ متى كان المدرّس واعيا بالرّهان ومتكوّنا في الميدان.

 

---

V ـ المراجع المعتمدة

 

• Jean., A propos du statut de l’erreur dans l’enseignement des mathématiques, Paris : Hachette, 2002, p.1.
• Alain., « que nous apprennent les erreurs de nos élèves » In, Alain, Bouvier (dir), Didactique des mathématiques, le dire et le faire, Paris : Editions Cedic, 1986, p. 117 et 125.
• Jean-Pierre., L’erreur, un outil pour enseigner, ESF éditeur, 1997, p.10-23.
• Briand, Joël et Chevalier, Marie–Claude., Les enjeux didactiques dans l’enseignement des mathématiques, Hatier, Paris, 1995, p. 109.
• Charnay, Roland., « l’erreur dans l’enseignement des mathématiques » In, en mathématiques peut mieux faire…l’élève face à la difficulté en mathématiques, Rencontres pédagogiques n°12, INRP, Paris, 1986, p. 9,10.
• Bachelard, G., La formation de l’esprit scientifique, contribution à une psychanalyse de la connaissance objective, Vrin, 10e éd. 1977, p.13.
• Fabre, Michel., Bachelard éducateur, Paris, PUF, 1995, p.85.
• Fabre, Michel., Situations-problèmes et savoir Scolaire, Paris, PUF, 1999, p160.
• Jean-Pierre, Ibid., p.109.
• Michel, Ibid., p.161, 162.
• Migne, Jean., « Pédagogie et représentation » In, Education permanente, 8, 1970, p 67-87.
• Astolfi, J-P et autres., Mots –clés de la didactique des sciences, De Boeck et larcier s.a, 1997, p 149 – 152.
• Astolfi, J.P et Develay, M., La didactique des sciences, Paris, PUF, 1989, p32.
• Houssaye, Jean (dir)., La pédagogie. Une encyclopédie pour aujourd’hui, Paris, ESF éditeur, 1994, p. 282.
• Raynal, F et Rieunier, A., Pédagogie : dictionnaire des concepts clés, Apprentissage, formation, psychologie cognitive, ESF éditeur, Paris 2^émeédition 1998, p.347-348.
• Charnay, Roland et Mante, Michel., « De l’analyse d’erreur en mathématiques aux dispositifs de re-médiation », quelques pistes…, In, REPERES-IREM, n°7-avril 1992, p.5.
• , p. 6.
• Brousseau, Guy., « obstacles épistémologiques en mathématiques » In, Recherches en Didactique des Mathématiques, Vol 4, n°2, 1983, p. 195.
• Baruk, Stella., « Le mal mathématique » In, le quotidien canadien : Le devoir, avril 1993.