تغيرت النظرة  للرياضيات و التي ترى أن التحصيل هو الهدف الأساسي لتعليم الرياضيات، فأصبحت تلك التي يستطيع الطالب من خلالها توظيف ما اكتسبه من معرفة رياضية في حل المشكلات التي تواجهه في المواقف المختلفة وفي خدمة المجتمع الذي يعيش فيه . ولقد أصبحت الرياضيات في حياتنا المعاصرة اليوم، أكثر أهمية وضرورة عما كانت عليه في الماضي، لأنها تستخدم في العديد من مجالات الحياة اليومية، مما يعني وجود أهداف عظيمة للرياضيات . وقد أكد المجلس الوطني لمعلمي الرياضيات (National Council of Teachers of Mathematics, 2000) على أن امتلاك مهارات القوة الرياضية والتفكير (المعرفة و ما بعد المعرفة)، هو المعيار الأساس لتعلم الرياضيات؛ وذلك يتضمن حتما مهارات الاستدلال و التفكير الإبداعي و الناقد، والقدرة على حل المشكلات غير الروتينية.

ولما كان التفكير الإبداعي ركيزة أساسية، فقد كان التركيز على الإبداع الرياضي و تعريفه أمرا مهما، إلا أن تعريفاته قد تعددت و تنوعت، وربما كان أغلبهم يعرفه على أنه إنتاج أكبر عدد من الأفكار واكتشاف الأنماط، وإدراك المشكلات  الرياضية النادرة المتنوعة بين الأقران، بالإضافة إلى كونه نشاطا عقليا  معقدا وهادفا، يوجه نحو رغبة قوية في التقصي والبحث، و يستوجب توليد أفكار وحلول لمشكلات تواجه العقل تؤدي إلى إحداث تفكير متفتح طلق يتسم بالعمق الذي يؤدي إلى إنتاج فريد إبداعي .

ومن منظور خبراء الرياضيات، يرى سيسوونو (Siswono, 2010)  أن التفكير الإبداعي يشير إلى مزيج من التفكير المنطقي والمتشعب (التباعدي) القائم على الحدس، ولكن لديه هدف واعٍ؛ فالتفكير المتباعد يركز على المرونة والطلاقة والأصالة في حل المشكلات، وينتج العديد من الأفكار يكون بعضها مفيد لإيجاد الحلول، بينما عملية التفكير المنطقي تستخدم لفحص الحلول المناسبة،  فهو يمثل منهجية وعملية عقلانية للتحقق والاستنتاج الصحيح.  لأن الطلاب لديهم خلفيات مختلفة ومختلفة القدرات ، لديهم إمكانات مختلفة في أنماط التفكير ، والخيال والأداء؛ لذلك يختلف الطلاب في مستويات التفكير الإبداعي.

علاوة على ذلك، فقد قدم إرفينك المذكور في سريرامان (Sriraman, 2004) ثلاث مراحل للإبداع الرياضي: المرحلة الأولى وهي التقنية الأولية (Stage 0) ويكون فيها التعامل مع المواقف الرياضية باستخدام القوانين والإجراءات دون وعي لأساسها النظري وقد تشمل التقنيات العملية؛ المرحلة الثانية وهي النشاط الخوارزمي (Stage 1) ويتم خلالها استخدام الإجراءات والحسابات من خلال صياغة صورة مفاهيمية لبنية المشكلة التي تنم عن فهم هذه البنية؛ والمرحلة الثالثة وهي النشاط الإبداعي (المفاهيمي والبنّاء) (Stage 2) وتكون فيها معالجة المشكلة و حلها من خلال وضع الفرضيات و اختبارها.

علاوة على ذلك، تمر العملية الإبداعية بمجموعة من المراحل المتتالية تؤدي إلي صيغة نهائية يُعبر عنها في صورة نتاج جديد غير مألوف؛ يفيد المجتمع، ويتصف بالاستمرارية، وحددت دراسات بعض الباحثين أمثال أوزبورن  (Osborn, 1964, 1991)و فريسمان (Fresman, 1996)  وتتلخص بأربعة مراحل متتالية كما وصفها بونكريه  (Poincare)كما يأتي:

المرحلة الأولى- مرحلة الإعداد Preparation Stage 

ويتم في هذه المرحلة جمع المعلومات والبيانات عن المشكلة، وتحديد المشكلة بدقة، ودراسة الظروف المحيطة بها، وتسجيل الملاحظات، وتسمى بالمرحلة الأولية للعمل الواعي.

المرحلة الثانية – مرحلة الاحتضان Incubation Stage 

هي المرحلة التي يتم فيها جمع المعلومات والبيانات عن المشكلة، وتنظيم هذه المعلومات وما بينها من علاقات، بالصور التي تجعل من السهل على المفكر أن يقترح أفكارا أو  حلولا، أو يضع فروضا لحل المشكلة، وتأتي هذه المرحلة بعد التفكير في المشكلة لفترة من الوقت دون الوصول إلي حل مُرضٍ؛ حيث يحدث إعادة تنظيم للمعلومات للبحث عن حلول.

المرحلة الثالثة – مرحلة الإشراق Illumination Stage 

وتسمى بلحظة الإلهام لحل المشكلة، وهذه الحالة لا يمكن تحديدها مسبقاً، وتلعب الظروف المكانية والزمنية والبيئة المحيطة دورا  في تحريكها، فهي الحالة التي تحدث فيها الومضة أو الشرارة  التي تؤدي إلي فكرة الحل، والخروج من المأزق، وهذه الحالة تحدث لدى الفرد دون سابق إنذار.

المرحلة الرابعة – مرحلة التحقيق Verification Stage 

وفي هذه المرحلة يتم التأكيد والتحقيق والتقويم لما وصل إليه الفرد من حلول أو وضع أفكار للمشكلة؛ بحيث تخضع الأفكار للدراسة واختبار مدى صحتها لحل المشكلة، والتحقق من منطقية الفكرة أو الحل، وهي المرحلة النهائية، ومرحلة الحصول على الإنتاج الجديد المختلف عملا أو فكرا، ويتجلى فيها الأداء ملموسا.

وللإبداع مستويات أو مهارات يجب مراعاتها، وقد وصفها البعض بأنها تمثل قدرات التفكير الإبداعي، وهي:

1. الطلاقة Fluency Skill : يرى تورانس و جاك  (Torrance & Jach, 1984)أن الطلاقة هي : القدرة على استدعاء أكبر عدد ممكن من الاستجابات تجاه مشكلة ما أو مثير معين، وذلك في فترة زمنية محددة، و تتمثل في قدرة الطالب على اكتشاف الأنماط و إكمالها  وتكوين أنماط جديدة.
2. المرونة Flexibility : يعرفها جيلفورد (Guilford, 1976) بأنها القدرة على سرعة إنتاج أفكار تنتمي إلى أنواع مختلفة من الأفكار التي ترتبط بموقف معين، أما محمد (2012) فيصفها بأنها تنوع أو اختلاف الأفكار التي يأتي بها الفرد، وهي القدرة على توليد أفكار متنوعة، ليست من نوع الأفكار والحلول الروتينية.
3. الأصالة  Originality : يرى جيلفورد (Guilford, 1976) بأن الأصالة هي الخروج عن المألوف والإتيان بأفكار جديدة لا تعتمد على كمية الأفكار بقدر ما تعتمد على نوعية تلك الأفكار، ويمكن للمعلم تنمية التفكير الإبداعي للمتعلمين من خلال تشجيع أصالة التفكير لديهم، وذلك بتشجيع تجدد وتفرد الأفكار من خلال الحث على وضع الحلول الممكنة لمشكلة ما أو مسألة ما مع تقبل جميع وجهات النظر، وما يصدر عنها من أفكار. وتشير محمد (2012) إلى أن الأسئلة التي يمكن من خلالها الكشف عن الأصالة؛ هي تلك الأسئلة التي تحمل إجاباتها استعمالات مثيرة وجديدة لأشياء عادية.

وقد أشار كل من  تريفنجر وإساكسن  (Treffinger & Isaksen, 2005)بالتعاون بين  سيدني بارنز مع أليكس أوزبورن في عام (1950) لتعديل وتطوير ما يسمى اليوم (نموذج أوزبورن بارنز للحل الإبداعي للمشكلات)؛ حيث قدما خمسة مراحل للنموذج  تم تجميعها في 3 مهارات رئيسة هي (فهم المشكلة، توليد الأفكار، التحضير للحل) كما يتضح في الشكل (1)، وقد قمت بإضافة (الطلاقة، الأصالة، والمرونة) على هذا المخطط ليناسب منحى STEM.

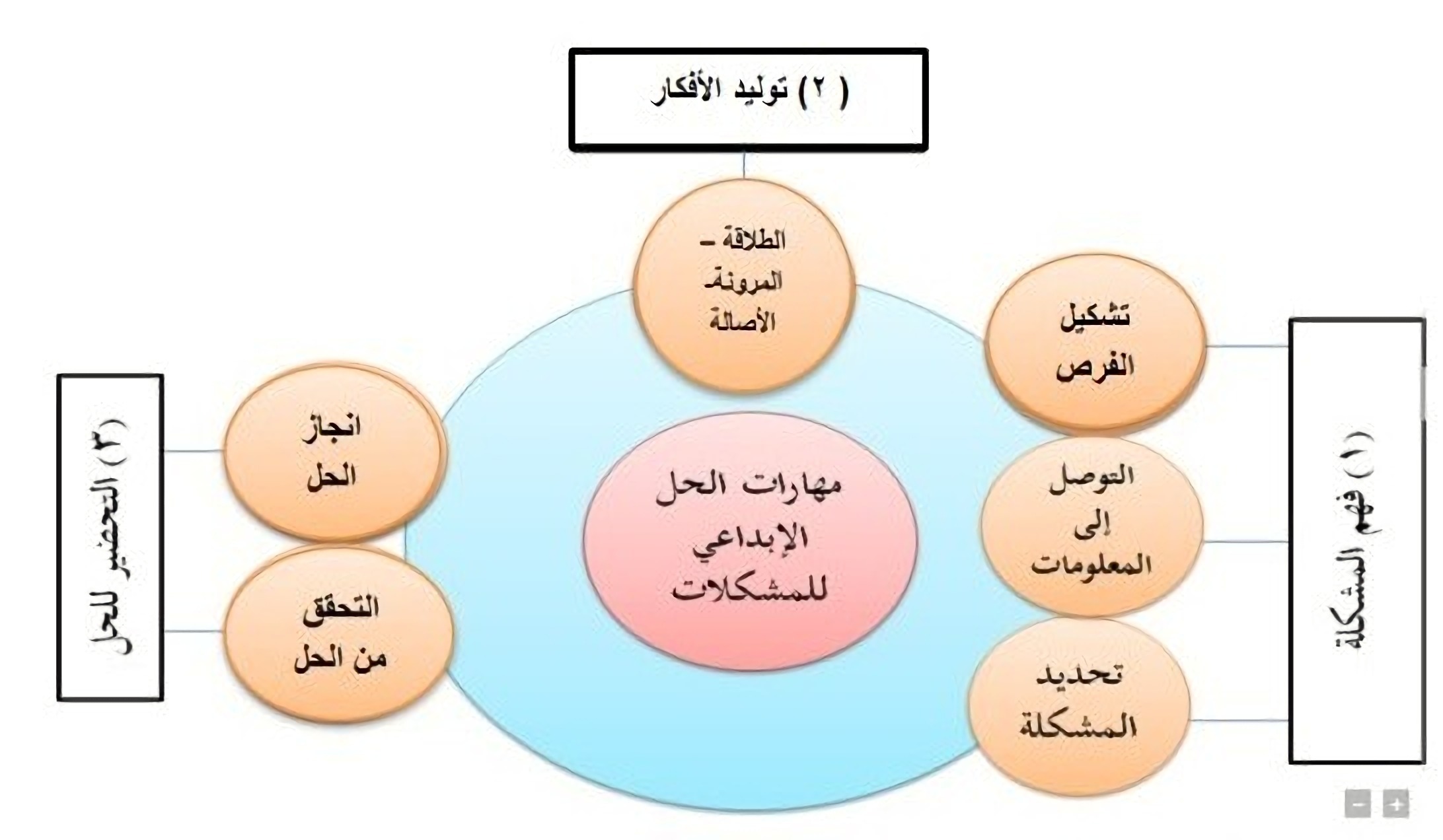
الشكل (1): مخطط  يوضح مهارات التفكير الإبداعي للمشكلات الرياضية

ولتنمية التفكير الإبداعي في الرياضيات -باعتباره إحدى مهارات التفكير الرياضي المتقدم- يقترح خطاب (2007) مراعاة بعض الأمور كأن يتضح أولاً في ذهن المعلم أن الإبداع من أهم أهداف تعليم وتعلم الرياضيات؛ تقديم المسائل والتدريبات ذات الحلول الجديدة التي تنمي الإبداع والابتعاد عن التدريب الروتيني؛ عرض مواقف رياضية محيرة تزيد من حماس الطالبات لحلها؛ طرح أسئلة مفتوحة النهاية؛ تدريب الطلبة على عمل وطرح أسئلة بأنفسهم؛ تقديم الرياضيات في إطار متكامل مع المواد الدراسية الأخرى؛ حل التمرينات الرياضية بأكثر من طريقة؛ مساعدة الطالبات على المشاركة الفعالة في مناقشة الأفكار الرياضية؛ و أخيرا إعطاء المعلمة أفكار وطرق جديدة لحل المشكلات الرياضية.

ومن المداخل الحديثة التي تدعم التطبيقات الواقعية لتعلم وتقويم الرياضيات و تعزيز التفكير الرياضي المتقدم؛ والتي تسهم في حل المشكلات التعليمية أو الاجتماعية أو الاقتصادية وغيرها من المشكلات ما يعرف بمدخل التكامل بين العلوم والتكنولوجيا والهندسة والرياضيات STEM(Science, Technology, Engineering, Mathematics)؛ فحل المشكلات الواقعية يتطلب معرفة الطالب كيفية الربط بين العلوم المختلفة ليستطيع من خلالها التوصل للابتكارات التي تسد الفجوات للتنمية المستدامة، وتسهم في تلبية حاجة سوق العمل، وغيرها من المهارات و المعارف و الاتجاهات ذات الصلة (Bureau, 2016) والشكل الآتي يوضح ذلك:

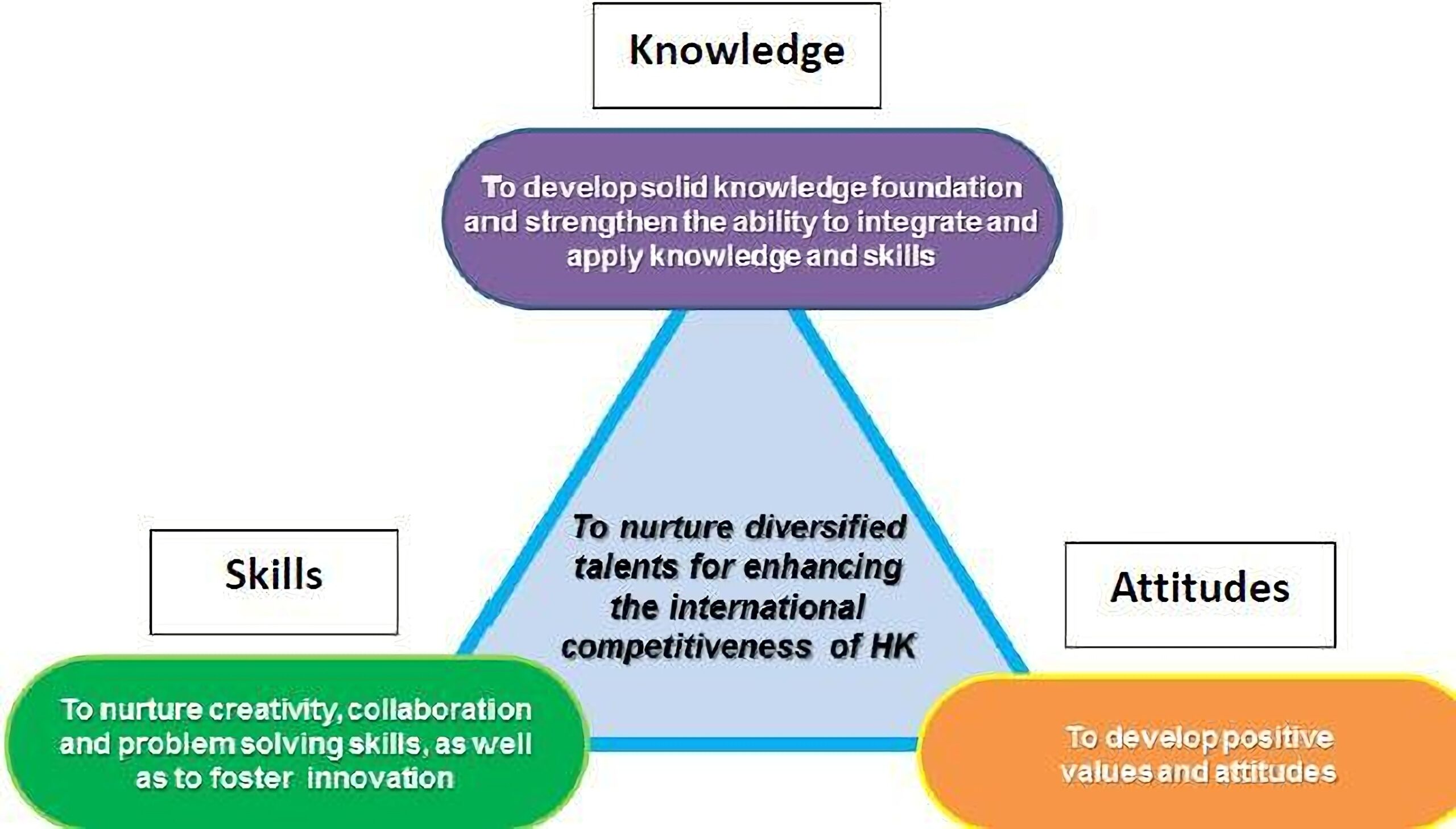
وانطلاقا من أسس النظرية البنائية، فقد وجدت أن منحى STEM يعزز التفكير الإبداعي؛ ذلك أن الركائز البنائية التي يتردد صداها مع تعليم STEM  وفق ما جاء في (Ronning, Bruning, Schraw, Norby, and Ronning, 2004) تركز على أن التعلم عملية بناءة منفتحة؛ و أن الدوافع و المعتقدات جزء لا يتجزأ من الإدراك؛ وأخيرا أن التعلم ينطلق من المعارف والاستراتيجيات والخبرات السياقية. و عليه فلو تبنى المعلم في تدريسه و تقويمه و إعداد الاختبارات منحى STEM سيعزز قدرات التفكير الإبداعي لدى الطلبة.

يرى (سوبر حوا، 2015) بأن STEM نظام تعلم وتعليم واستراتيجية تقويم؛ يقوم بشكل أساسي على البحث و التفكير و حل المشكلات، والتعلم من خلال المشروعات التي من خلالها يطبق الطالب ما يتعلمه في العلوم و الرياضيات والهندسة باستخدام التكنولوجيا. وعليه فإن مدخل STEM هو اختصار لأربعة علوم معرفية (Science, Technology, Engineering, Mathematics) تتطلب التكامل في تعلمها وتعليمها وتفعيلها أثناء التقويم، كما تتطلب تجهيز البيئة التعليمية في سياق العالم الحقيقي، بحيث تمكن الطلبة من الوصول إلى المعرفة الشاملة والمترابطة للموضوعات المتعلقة بها بعيداً عن المفاهيم النظرية التي يتلقونها بصورة تقليدية داخل الفصول الدراسية.

و قد أشارت غانم (2012) إلى أن STEM يعتمد على التمحور حول الخبرات المفاهيمية المتكاملة، والتمركز حول حل المشكلات والتقصي و تطبيق الأنشطة العملية بشكل مكثف؛ بالإضافة الى التقويم الواقعي الأصيل بأبعاده المتعددة المستندة على معايير الأداء؛ والتركيز على قدرات التفكير الإبداعي و الناقد، بالإضافة إلى اهتمامه بمهارات ما وراء المعرفة.

وهنا – ومن وجهة نظري- فلا مجال لإغفال القاعدة الأساس، وهي أنه من يملك فهما صحيحا وصورا ذهنية صحية للمفاهيم بتمثيلات متنوعة، تكون الشبكة المفاهيمية لديه منظمة، وبالتالي عمليات التفكير لديه منظمة ومتقدمة، وتزيد احتمالية قدرته على التفكير الإبداعي بشكل كبير، وعندها قد تأتي الومضات الإبداعية من الحدس الذي يشرق أحيانا دون سابق إنذار، ولكن الفهم السليم و العمل الجاد هو الأساس، وعدم الاستهانة بأي فكرة تخطر ومحاولة إثبات أصالتها، عن طريق إعطاء أمثلة و أمثلة مضادة مثلا، كما أن ابتداع طرق أصيلة مرنة وفيها طلاقة يتطلب مستوى عالٍ من الفهم و المثابرة و التأمل و تطبيق للعمليات ما وراء معرفية أثناء التفكير بطرق حل إبداعية وهذا ما ضمنه منحى STEM.
المراجع

المراجع العربية:

خطاب، أحمد علي إبراهيم (2007). أثر استخدام إستراتيجية ما وراء المعرفة في تدريس الرياضيات على التحصيل وتنمية التفكير الإبداعي لدى تلاميذ الحلقة الثانية من التعليم الأساسي، رسالة ماجستير، كلية التربية، جامعة العلوم.

غانم، تفيدة سيد (2012). تصميم مناهج المتفوقين في ضوء مدخل STEM (العلوم-التكنولوجيا-التصميم الهندسي-الرياضيات) في المرحلة الثانوية، المركز القومي للبحوث التربوية والتنمية، شعبة بحوث تطوير المناهج، مصر .

سوبر، حوا (2015): ماذا تعرف عن نظام التعليم الحر “STEM“؟.   مسترجع من : WWW.alaraby.co.sup

محمد، سحر عبده (2012). برنامج قائم على محاكاة الهندسة التفاعلية بالحاسوب وأثره في التحصيل و تنمية التفكير الإبداعي و الدافع للإنجاز لدى تلاميذ المرحلة الابتدائية، رسالة دكتوراة، كلية التربية، جامعة بور سعيد .

Bruning, R. H., Schraw, G. J., & Ronning, R. R. (1999). Cognitive psychology and instruction. Prentice-Hall, Inc., One Lake Street, Upper Saddle River, NJ 07458. Bureau, E. (2016). Report on promotion of STEM education: Unleashing potential in innovation. Hong Kong: Education Bureau.

Bureau, H. K. E. (2015). Promotion of STEM Education—Unleashing Potential in Innovation. Curriculum Development Council: Hong Kong, 1-24., Retrieved from:

http://www.edb.gov.hk//attachment/en/curriculum-development/renwalBrief%20STEM%20(Overview)_eng_20151105.pdf

Rowland, G. (1995). Instructional design and creativity: A response to the criticized. Educational Technology, 35(5), 17-22.

Guilford, J. P. (1967). The Nature of Human Intelligence. New York: Mc Graw Hill, USA.

Fresman, R. D (1996). Improving Higher Order Thinking of Middle School by Teaching Skills Directly. Handbook of Creativity, Nove University Press.

NCTM. (2000). Principles and Standards for School Mathematics. National Council of Teachers of Mathematics.

Osborn, A. F. (1964). How to become more Creative, New York: Charles Scribner’s Sons.

Osborn, R. E. (1991). Creative disarray: Models of ministry in a changing America. Chalice Pr.

Siswono, T. Y. E. (2010). Leveling students’ creative thinking in solving and posing mathematical problem. Journal on Mathematics Education, 1(1), 17-40.

Sriraman, B. (2004). The Characteristics of Mathematical Creativity. The Mathematics Educator. Volume 14. Number I, 2004 pp.19-34. Retrieved September 10, 2005, from:

 http://jwilson.coe.uga.edu/DEPT/TME/Issues/v14n1.sriraman.pdf.

Torrance, E. P. (1971). The creative person. The encyclopedia of education, 552-557.

Torrance, E. P., & Presbury, J. (1984). The criteria of success used in 242 recent experimental studies of creativity. Creative Child & Adult Quarterly.

Treffinger, D. J. & Isakesen, S. G. (2005). Creative Problem Solving: The History, Development, and Implications for Gifted Education and Talent Development. The Gifted child Quarterly, 49(4), 342-353.