المقدمة:

يعتبر مفهوم الاقتران الرياضي واحدا من المفاهيم الأساسية للرياضيات، حيث تمّ استخدام الاقتران للتنوع المشترك والعلاقات بين المقادير الرياضية، و في الرسوم البيانية والجداول الفلكية. كما تمّ الاعتماد على مفهوم الاقتران الرياضي في حساب التفاضل والتكامل، ويعتبر مقدمة لمفهوم الجبر الرمزي، كما إن لمفهوم الاقتران دورا هاما في إنشاء ارتباط قوي بين الجبر والهندسة (Viirman,2014).

وأشار ماكوني (Makonye,2014) إن مفهوم الاقتران هو واحد من أكبر الأفكار التي تبني نظام الرياضيات لأنه المادة التي تحافظ على المفاهيم والإجراءات الرياضية الأساسية. ولكن غالبًا ما يتم إساءة فهم مفهوم الاقتران من قبل المعلمين والمتعلمين. غالبًا ما يتم تدريس مفهوم الاقتران دون علاقة بالسياق اليومي. ويلجأ المعلمون التقليديون على تقديم رمزية رياضية رسمية لمفهوم الاقتران مثل (f (x في بعض الأحيان قبل الأوان للمتعلمين، مما قد يؤدي إلى قيام بعض الطلبة بتطوير مفاهيم خاطئة عن مفهوم الاقتران. وهذا يقودنا إلى الانتباه لما  أشار إليه تال و فينر (Tall,Vinner,1981) حول صورة المفهوم وتعريف المفهوم. يقترحون أنه عندما نفكر في مفهوم ما يتم إثارة شيء في أذهاننا. غالبًا لا تتعلق هذه الصور بالضرورة بتعريف المفهوم حتى إذا تم تعريف المفهوم من الناحية المفاهيمية بشكل جيد. تسمى مجموعة المفاهيم صورة المفهوم. فإن صورة المفهوم هي البنية المعرفية الكاملة المرتبطة بالمفهوم.

من المهم جدًا تحديد وتصحيح الأخطاء التي يرتكبها الطلاب حول المفاهيم الرياضية. ومن هذه الدراسات المتعلقة بمفهوم الاقتران دراسة كانيز و لسلين و كشك (Cansiz,kucuk & Lsleyen, 2011) والتي هدفت للكشف عن المفاهيم الخاطئة لدى طلاب المدارس الثانوية حول الاقترانات في العام الدراسي 2009-2010. تم جمع بيانات البحث 61 طالبًا من طلاب الصف التاسع والعاشر والحادي عشر و الذين تم اختيارهم بشكل عشوائي، وتكونت أدوات جمع البيانات من اختبار تحصيلي وإجراء مقابلات. وحدد الباحثون أربعة مجالات لمفهوم الاقتران وهي: مفهوم الاقتران من خلال الرسم البياني، أو التعبير اللفظي، أو جداول البيانات، وأخر مجال من خلال الجبر، وكانت النتائج أن الطلاب يرتكبون أخطاء لفهم ما إذا كان الرسم هو رسم اقتراني أم لا، إضافة عدم القدرة في تحديد مفهوم الاقتران من خلال استخدام جداول البيانات.

وتلعب التعريفات في الرياضيات دورَ مهيمن في بناء التفكير والمفاهيم الرياضية. حيث تأثر الصور المفاهيمية على معنى المفاهيم. وتنسق الصور بشكل أكبر مع تعريف المفهوم المقبول، والذي بدوره يعزز التفكير لدى الطلاب. و يمكن دراسة مفهوم للاقتران بناءً على ثلاثة أدلة: (1) أفكار الطلبة عن الاقتران، (2) قدرتهم على التعرف على الاقترانات في أشكال مختلفة من التمثيل، و (3) حل المهمات التي تنطوي على تحويل الاقتران من تمثيل إلى آخر(anaoura, A., Michael-Chrysanthou, P., & Philippou, A.، 2015).

وأشار رومبرغ وفينيم و كاربنتر Romberg, T. Fennema, E . & Carpenter, T ,1993) ) وجود أكثر من صورة لمفهوم الاقتران، فقد تم تحديد  مفهوم الاقتران من خلال: قيم المدخلات والمخرجات، الرسم البياني،  المجال والمدى، التعبير اللفظي، الصيغة الجبرية، والجداول، واستخدام الأنماط .

تم إعداد المهمات بناءً على الأدب السابق، وهدفت هذه المهمات لتحديد الأخطاء المفاهيمية التي يمتلكها الطلبة حول مفهوم الاقتران. وطرق التفكير وطرق الفهم التي يمتلكها الطلبة للإجابة على المهمات. ومن الدراسات التي اهتمت بمفهوم الاقتران دراسة امبرص و فيلر و فانسكو (Ambrus, Filler & Vansco,2018)، ودراسة لاجرنج و مينه (Lagrange, Minh, 2010)، ودراسة ماكوني (Makonye,2014), ودراسة كانيز و لسلين و كشك (Cansiz,kucuk & Lsleyen, 2011).

بيّن بن (Ben, 2006) إجراءات تحليل الأخطاء المفاهيمية والصور الذهنية للطلبة حول المفاهيم الرياضية ومنها: جمع إجابات الطلبة على المهمات المتعلقة بالمفهوم الرياضي. و الطلب من الطلاب التفكير بصوت مسموع عند حل المهمات. ثم يقوم المعلم بتسجيل إجابات الطلبة المكتوبة والمسموعة. و تحليل إجابات الطلبة، وتحديد الأخطاء المفاهيمية التي ارتكبوها. وأخيرا إجراء مقابلات مع الطلبة، وهدفها تفسير كيفية الإجابة على المسائل وبالتالي التحقق من الأخطاء المفاهيمية والصور الذهنية التي يمتلكوها.

سيتم التعرف على الأخطاء المفاهيمية والصور الذهنية لمفهوم الاقتران الرياضي لدى الطلبة، و طرق الفهم وطرق التفكيرلديهم من خلال طرح مجموعة من المهام/ وتوقع الغجابة عليها بناءً على الخبرة في التدريس.

المهمة 1:

إذا أردت فتح بريدك الإلكتروني الخاص بك، فإنه يتطلب منك إدخال اسم المستخدم و كلمة المرور، هل العلاقة بين اسم المستخدم وكلمة المرور تسمى اقترانا؟ برّر أجابتك.

• الإجابة: نعم اقتران، لأن لكل اسم مستخدم كلمة مرور واحدة، وليس لدى الايميل كلمات مرور متعددة، وإنما كلمة واحدة فقط.

المهمة 2:

إذا علمت إن لكل دولة رمز اتصال دولي، فإذا أراد صديقك الاتصال من خارج الأردن يجب أن يضيف رمز الاتصال الدولي الخاص بالأردن 00962 إلى رقم هاتفك، هل تعتبر العلاقة بين الدولة ورمز الاتصال الدولي اقتران؟ برّر إجابتك.

• الإجابة: نعم اقتران، لأن لكل دولة رمز اتصال دولي واحد خاص بها فقط، ولا يوجد دولة لها أكثر من رمز اتصال دولي.

المهمة 3:

نظم جدولا يبين اسم الشهر وعدد أيامه مع مراعاة السنة العادية والكبيسة، هل العلاقة بين الشهر وعدد الأيام اقتران؟ برّر أجابتك.

• الإجابة: ليس اقتران، لأن شهر 2 له قيمتين هما: 28، 29.
• إجابة متوقعة: نعم اقتران، بدون الانتباه إن عدد أيام شهر 2 قد تكون 28 (السنة العادية) أو 29 ( السنة الكبيسة).

المهمة 4:

يُقدم مذيع النشرة الجوية لمدينة إربد- الأردن، ويبين درجات الحرارة للمدينة  يوم السبت  11/4/2020، وكما يوضح الشكل.

• هل تعتبر العلاقة بين تاريخ اليوم ودرجة الحرارة اقتران؟ برّر إجابتك.
• كيف يمكن جعل العلاقة بين تاريخ اليوم ودرجة الحرارة اقترانا.

 

• الإجابة: العلاقة ليست اقتران، قد تتغير درجة الحرارة بشكل كبير على مدار اليوم واحد، أي أن درجات الحرارة تختلف من وقت إلى أخر ضمن اليوم الواحد.
• الإجابة المتوقعة: العلاقة اقتران، بناءً على خطأ مفاهيمي.

المهمة 5:

قام أحد أصحاب المصانع بحساب التكلفة الكلية السنوية للمصنع فوجد أنها تتبع العلاقة ( 540 + 1.37 س) دينار، حيث تمثل س كمية الإنتاج، أجب عن الأسئلة التالية:

• أكمل المخطط التالي:

• مثّل العلاقة بيانيا.
• ما يدفعه صاحب المصنع سنويا إذا أنتج 1000 قطعه في السنة.
• ما يدفعه صاحب المصنع إذا لم ينتج المصنع أي كمية.

د. هل تمثل العلاقة اقتران؟ برّر إجابتك.

المهمة 6: 

• جد المجال والمدى لكل من العلاقات التالية. و بين أي من العلاقات الآتية تمثل اقترانا؟
• ع = } (3، 1)، ( 4،2)، (3، 5){
• هـ = } (1، 4)، ( 3،2)، (2، 5)، (4، 1) {

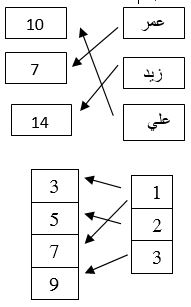
• الجواب: 1. اقتران. ليس اقتران.    3. اقتران      4. ليس اقتران.

المهمة 7:

استخدام أعواد الثقاب، أكمل نمط الأشكال المعطى.

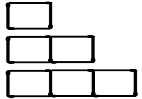
• ابحث عن عدد أعواد الثقاب اللازمة لإنشاء 5 مربعات.
• ابحث على عدد المربعات التي يمكن إجراؤها بواسطة 96 أعواد الثقاب
• ارسم الرسم البياني لتمثيل العلاقة بين عدد المربعات وعدد أعواد الثقاب.
• هل العلاقة بين عدد المربعات وعدد أعواد الثقاب اقترنا؟ ولماذا؟
• ما قاعدة العلاقة إذا كانت العلاقة اقترانا.
• الجواب: القاعدة هي : 3 س + 1

المهمة 8:

يعمل خالد في أحد المطاعم بدوام جزئي بحيث يعتمد راتبه الأسبوعي على عدد الساعات التي يعملها، إذا كان يتقاضى 1.5 دينار عن كل ساعة عمل.

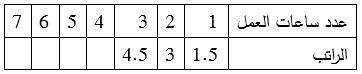
1. أكمل الجدول المعطى.
2. ما راتبه إذا عمل 8 ساعات، 15 ساعة، 25 ساعة.
3. إذا تقاضى خالد 39 ديناراً فكم ساعة عمل.
4. أكتب علاقة (أزواج مرتبة) بين عدد ساعات العمل، والراتب الذي يتقاضاه خالد.
5. هل راتب خالد اقتران في عدد ساعات العمل. وما قاعدته.

المهمة 9:  

بين إن كانت كل من العلاقات الممثلة بالرسم البياني اقتراناً أم لا، ثمّ برّر إجابتك.

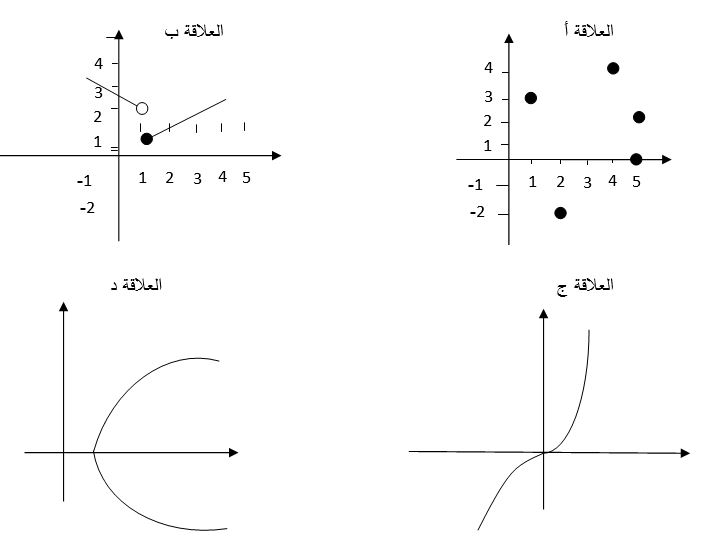
• الجواب: العلاقة أ و د ليست اقتران، والعلاقة ب وجـ اقتران.

المهمة 10:  

لديك العلاقة الجبرية التالية ( ص = 3 س – 12 )، أجب عما يلي:

1. مثّل العلاقة بيانياً.
2. ما المجال والمدى للعلاقة.
3. هل العلاقة تمثل اقترانا، برّر إجابتك؟
4. ما خصائص العلاقة ( متزايد، متناقص).
5. ما صفر الاقتران.
6. ما هو المقطع السيني والمقطع الصادي.

 

الصور الذهنية لمفهوم الاقتران وطرق الفهم والتفكير:

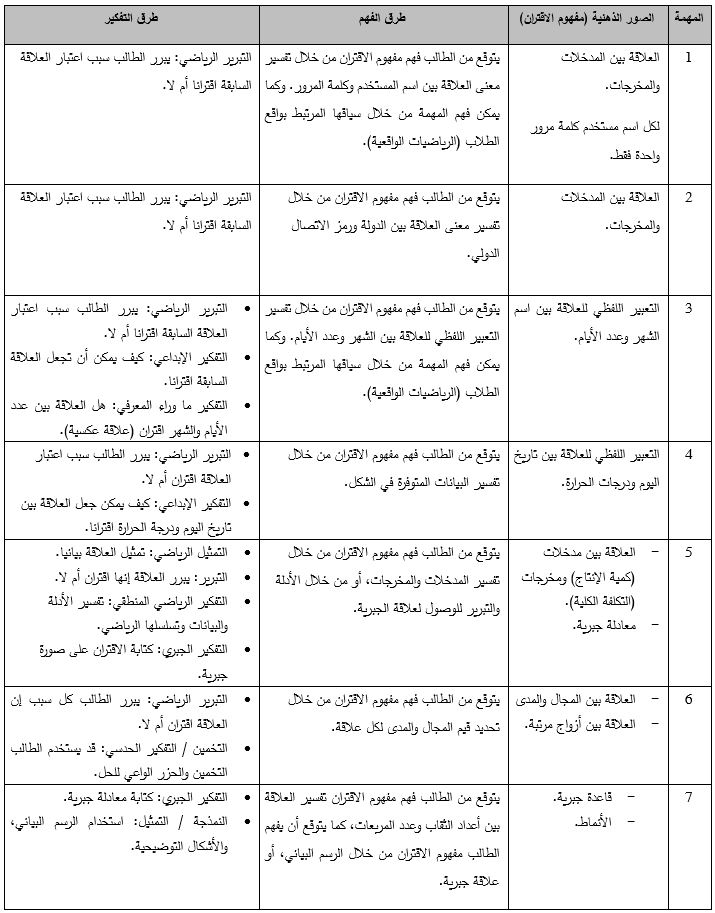
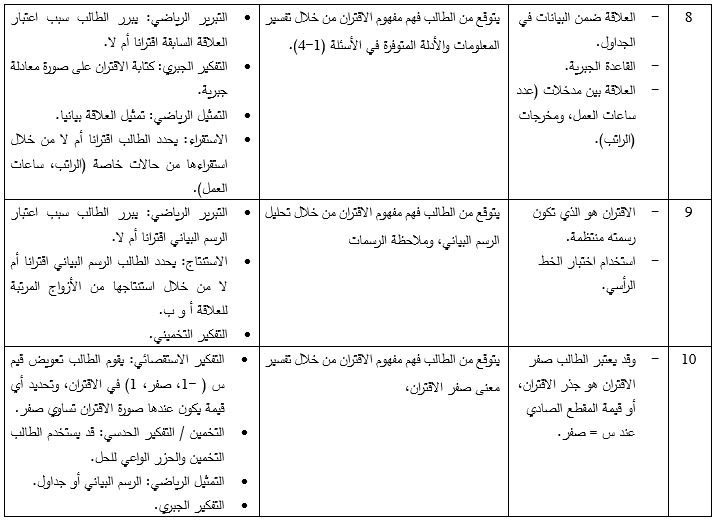
نبين بعض من الأخطاء المفاهيمية التي قد يقع بها الطلبة في التعامل مع الاقتران، إضافةً بعض طرق علاجها.

الأخطاء المفاهيمية وعلاجها:

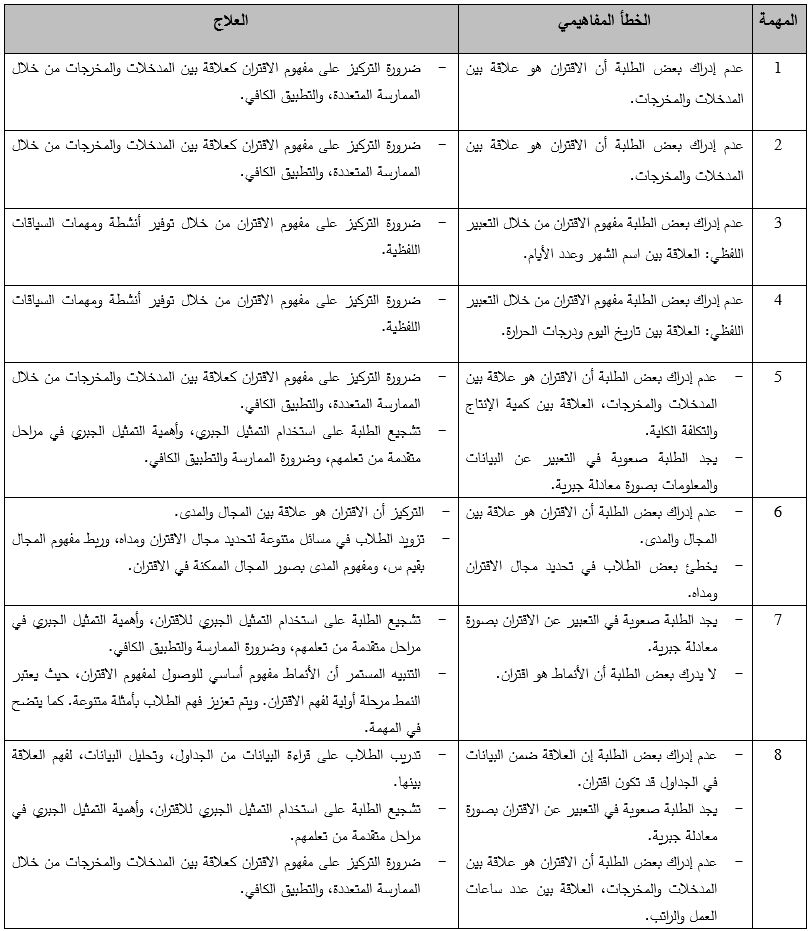
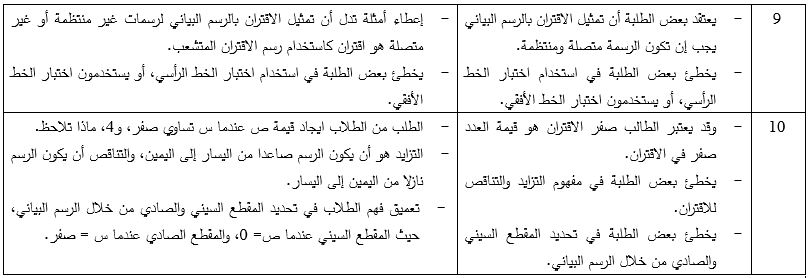
المراجع:

Ambrus, G. Filler, A.& Vancso,o (2018). Functional Reasoning and working with Functions: Function\ Mapping in mathematics teaching tradition in Hungary and Germany. The mathematics Enthusiast, 15(3) , 429-454.

Ben-Hur,M (2006). Concept-Rich Mathematics Instruction. Alexandria: USA,ASCD.

Cansiz, S. kucuk, B.& Lsleyen,T (2011). Identify the Second school students Misconceptions about Functions. Procedia Social Behavioral Science, 15, 3837-3842.

Lagrange,J. Minh, T (2010). Approaching Functions Via Multiple Representation: A teaching Experiment With Casyopee. CERME France 6. 1^st 2009. 559-568.

Makonye, J (2014). Teaching Functions Using a Realistic Mathematics Education Approach: A Theoretical Perspective. International Journal Education Science. 7 (3). 653-662.

Panaoura, A., Michael-Chrysanthou, P., & Philippou, A. (2015, February). Teaching the concept of function: Definition and problem solving.‏  https://www.researchgate.net/publication/294718626.

Tall, D. Vinner, S. (1981). Concept image and concept definition with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151-169.

Viirman,o (2014). The Function concept and university mathematics teaching. Unpublished Dissertation. Karlsted University. Sweden.

Romberg, T. Fennema,E . & Carpenter, T (1993). Integrating Research on the Graphical Representation of Functions. New Jersey (1st): by Lawrence Erlbaum Associates Inc Publishers.